Earlier we defined deformation as the changes a body undergoes in the presence of a stress field and introduced the elastic and viscous relationships with stress. In this chapter we expand on this by looking at the behavior of natural materials and a range of response, as well as define the central tenet of modern tectonics: the lithospheric plate.

Whereas it is evident that there is no strain without stress, the relationship between stress and strain is not easy to define on a physical basis. In other words, realizing that stress and strain in rocks are related is quite a different matter from physically determining their actual relationship(s). In materials science and geology we like to use the term rheology (from the Greek rheos, meaning stream or flow) to describe the ability of stressed materials to deform, or flow, using fundamental parameters including as strain rate, elasticity and viscosity. These and related concepts will return in this chapter, where we focus on their significance for understanding natural rock deformation. First, we refresh your memory of the key concepts that were introduced earlier and that are used throughout this chapter, with the goal to help you navigate through more advanced rheologic behaviors:

Elasticity	Recoverable (non-permanent), instantaneous strain.
Fracturing	Deformation mechanism by which a rock body or mineral loses coherency by simultaneously breaking many atomic bonds.
Nonlinear viscosity	Permanent strain accumulation where the stress is exponentially related to the strain rate Plasticity Deformation mechanism that involves progressive breaking of atomic bonds without the material losing coherency (also non-Newtonian viscosity).
Strain rate	Rate of strain accumulation (ė, elongation, e, over time, t); shear strain rate, γ˙ (gamma dot), is twice the longitudinal strain rate.
Viscosity	Non-recoverable (permanent) strain that accumulates with time; the strain rate–stress relationship is linear (also, Newtonian viscosity).

Rheology is the study of flow of matter. Flow is an everyday phenomenon and in a previous chapter we used syrup on pancakes and human motion as day-to-day examples of deformation. Rocks don’t seem to change much by comparison, but remember that geologic processes take place over hundreds of thousands to millions of years. For example, yearly horizontal displacement along the San Andreas Fault (a strike-slip fault zone in California) is on the order of a few centimeters, so considerable deformation has accumulated over the last 700,000 years. Likewise, horizontal displacements on the order of tens to hundreds of kilometers have occurred in the Paleozoic Appalachian fold-and-thrust belt of eastern North America over time period of a few million years (m.y.). Geologically speaking, time is available in large supply, and given sufficient amounts of it, rocks are able to flow, not unlike syrup. Glacier ice offers an example of flow in a solid material that shows relatively large displacements on human time scales (Figure 5.1). The flow of window glass, on the other hand, is an urban legend that you can refute with the information presented in this chapter. We start by looking at the response to stress of a natural rock in a laboratory setting.

ROCK CREEP CURVE

Compression tests on rock samples illustrate that the behavior of rock to which a load is applied is not simple. Figure 10.1a shows what is called a creep curve, which plots strain as a function of time during the experiment, while the differential stress is held constant.

FIGURE 10.1. The creep curve. (a) Generalized strain–time curve, which shows primary (I), secondary (II), and tertiary (III) creep. With continued stress the material will fail; (b) if we remove the stress, the material relaxes, while permanent strain remains. [5.2]

Three creep regimes are observed:

Primary or transient creep, during which strain rate decreases with time following very rapid initial accumulation.
Secondary or steady-state creep, during which strain accumulation is approximately linear with time.
Tertiary or accelerated creep, during which strain rate increases with time; eventually, continued loading will lead to failure.

Expressing these regimes in terms of strain rate, we move from decreasing strain rate to constant strain rate to increasing strain rate. Rather than continuing our creep experiment until the material fractures, we remove the stress sometime during the interval of steady-state creep. The corresponding creep curve for this second experiment is shown in Figure 10.1b. We see a rapid drop in strain when the stress is removed, after which the material relaxes a little more with time. Eventually there is no more change with time but, importantly, permanent strain remains. In order to examine this behavior of natural rocks we turn to simple analogies and use rheologic models.

LINEAR RHEOLOGIES

In describing various rheologic relationships, we earlier divide the behavior of materials into two types: elastic behavior and viscous behavior. Models and stress-strain(/strain rate) relationship are summarized in Figure 10.2a and b, in which the ratio of stress over strain or stress over strain rate is a constant.

FIGURE 10.2. Models of linear rheologies, using combinations of elasticity and viscosity. Physical models consist of strings and leaky pistons, and associated strain–time, stress–strain, or stress–strain rate curves are shown for (a) elastic, (b) viscous, (c) visco-elastic, and (d) elastico-viscous behavior. A useful way to examine these models is to trace the strain–time curves by considering the behavior of the spring and leaky piston individually, and their combinations. Symbols used: e = elongation, ė = strain rate, σ = stress, E = elasticity, η=viscosity, t = time, el is elastic component, vi is viscous component. [5.3]

For each rheologic model illustrated in Figure 10.2 we offer a physical analog, a creep (strain–time) curve and a stress–strain or stress–strain rate relationship, which will assist you with the descriptions below. Such equations describing the relationships between stress, strain, and strain rate are called constitutive equations. Earlier we examined elastic and viscous behavior, but we need to turn to their combinations to obtain a better match to the creep curve above.

Visco-elastic Behavior

Consider the situation in which the deformation process is reversible, but in which strain accumulation as well as strain recovery are delayed; this behavior is called viscoelastic behavior, also known as firmo-viscous or Kelvinian behavior [1]. A simple analog is a water-soaked sponge that is loaded on the top. The load on the soaked sponge is distributed between the water (viscous behavior) and the sponge material (elastic behavior). The water will flow out of the sponge in response to the load and eventually the sponge will support the load elastically. For a physical model we place a spring (elastic behavior) and a dash pot (viscous behavior) in parallel (Figure 10.2c). When stress is applied, both the spring and the dash pot move simultaneously. However, the dash pot retards the extension of the spring. When the stress is released, the spring will try to return to its original configuration, but again this movement is delayed by the dash pot.

The constitutive equation for viscoelastic behavior reflects the addition of the elastic and viscous components:

σ = E ⋅ e + η ⋅ ė Eq. 10.1

Elastico-viscous Behavior

Particularly instructive for understanding earth materials is elastico-viscous behavior, also called Maxwellian behavior [2], where a material behaves elastically at the first application of stress, but then behaves in a viscous manner. When the stress is removed the elastic portion of the strain is recovered, but the viscous component remains. We can model this behavior by placing a spring and a dash pot in series (Figure 10.2d). The spring deforms instantaneously when a stress is applied, after which the stress is transmitted to the dash pot. The dash pot will move at a constant rate for as long as the stress remains. When the stress is removed, the spring returns to its original state, but the dash pot remains where it stopped earlier.

The constitutive equation for this behavior, which is not derived here, is:

ė = σ˙/E + σ/η Eq. 10.2

where σ˙ is the stress per time unit (or, stress rate).

When the spring is extended, it stores energy that slowly relaxes as the dash pot moves, until the spring has returned to its original state. The time taken for the stress to reach 1/e times its original value is known as the Maxwell relaxation time, with e the base of natural logarithm (e = 2.718). Stress relaxation in this situation decays exponentially. The Maxwell relaxation time, tM, is obtained by dividing the viscosity by elasticicty (the shear modulus, or rigidity), which has time as unit:

tM = η/G Eq. 10.3

(is σ/ė ÷ σ/e = t)

In essence, the Maxwell relaxation time reflects the balance between viscosity and elasticity, with:

elastic behavior < tM < viscous behavior.

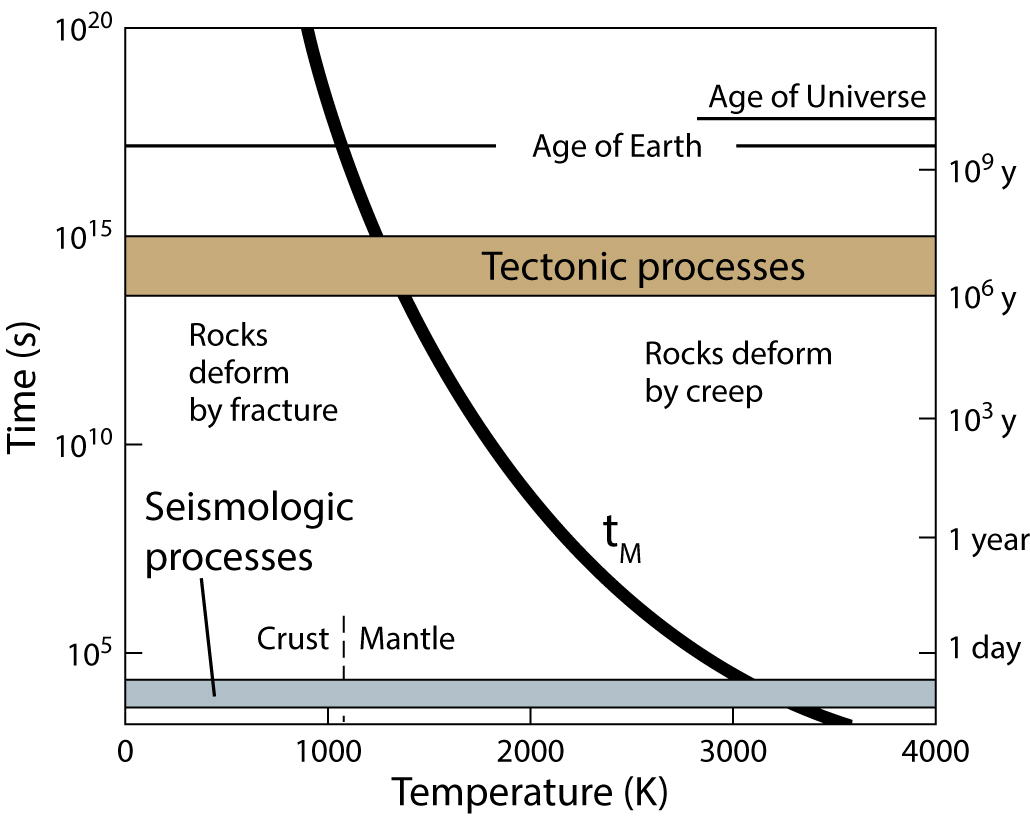
If tM is large then elasticity is relatively unimportant, and vice versa. Because viscosity is temperature dependent, tM can be expressed as a function of temperature. Figure 10.3 graphs this relationship between temperature and time for representative rock properties and shows that mantle rocks typically behave in a viscous manner (as a sticky fluid). The diagram also shows that shallow crustal rocks fail by fracture (elastic field), but lower crustal rocks deform by creep as well. This discrepancy reflects the detailed properties of crustal materials and their viscosities, as discussed later.

FIGURE 10.3. The Maxwell relaxation time, tM, plotted as a function of time and temperature. The curve is based on experimentally derived properties for rocks as a function of these variables.

The diagram predicts that hot mantle rocks deform as a viscous medium over long time intervals (tectonic processes), whereas cooler crustal rocks tend to deform by failure, especially over short time intervals (seismologic processes), which match our observations. [5.4]

Maxwell proposed this model to describe materials that initially show elastic behavior, but given sufficient time display viscous behavior, which matches the behavior of Earth rather well. Recall that seismic waves are elastic phenomena (acting over short time intervals) and that the mantle is capable of flowing in a viscous manner over geologic time (acting over long time intervals). Taking a mantle viscosity of 1021 Pa⋅s and a rigidity of 1011 Pa, and assuming an olivine-dominated mantle, we get a Maxwell relaxation time for the mantle of 1010 s, or on the order of 1000 years. This duration agrees well with the uplift that we see following the melting of thick continental glaciers after the last Ice Age, which resulted in uplift of regions in the northern countries over thousands of years after the glaciers retreated. We also get a sense of the deep flow stress of a deforming Earth from mantle viscosity and geologic strain rate (= η . ė), which is ~10 MPa, so much, much smaller than the lithostatic pressure at these depths.

General Linear Behavior

With combinations of two fundamental behaviors and after further tuning we arrive at a physical model that closely approaches that of the rock experiment, while still using linear rheologies. This is called general linear behavior, which is modeled by placing the elastico-viscous and viscoelastic models in series (Figure 10.4).

FIGURE 10.4. General linear behavior, as represented by a physical model consisting of strings and leaky cylinders, with associated strain–time curve. Symbols used: e = elongation, t = time, el is elastic component. [5.3]

Elastic strain accumulates at the first application of stress (the elastic segment of the elastico-viscous model). Subsequent behavior displays the interaction between the elastico-viscous and viscoelastic models. When the stress is removed, the elastic strain is first recovered, followed by the viscoelastic component. However, some amount of strain (permanent strain) will remain, even after long time intervals (the viscous component of the elastico-viscous model). The creep (e–t) curve for this general linear behavior is shown in Figure 10.4 and closely mimics the creep curve that was observed in experiment on natural rocks (compare with Figure 10.1b). We do not present the lengthy equation describing general linear behavior, but from the physical model you can see that the relevant equations involves the addition of visco-elastic and elastico-viscous behavior.

DEFORMATION ENVIRONMENTS

The creep curve showed us how natural rocks behavior under stress. But what about the environmental conditions of deformation? We look at the effects of variations in pressure, temperature, time, using rock deformation experiments that allows us to simulate and extrapolate to natural conditions in the Earth’s lithosphere. The reason for doing experiments on natural rocks is twofold, (1) we observe the actual behavior of rocks rather than that of syrup or elastic bands, and (2) we can control environmental parameters in experiments to examine their role in rock deformation. A vast amount of experimental data is available to us and many of the principles have, therefore, been known for several decades. Here we will limit our discussion by looking only at experiments that highlight particular parameters. By combining the various responses, we can begin to understand the rheology of natural rocks.

An alternative approach to examining the flow of rocks is to study material behavior in scaled experiments. Scaling brings fundamental quantities such as length [l], mass [m], and time [t] to the human scale. For example, we can use clay as a model material to study faulting, or wax to examine time-dependent behavior. Each analog that is used in scaled experiments has advantages and disadvantages, and the experimentalist has to make trade-offs between experimental conditions and geologic relevance. However, we will not use scaled experiments in this chapter.

Deformation Apparatus

A deformation experiment on a rock or a mineral can be carried out readily by placing a small sample in a vise, but when you try this experiment you have to be careful to avoid being bombarded with randomly flying chips as the material fails. If you ever cracked a hard nut in a nutcracker, you know what we mean. In rock deformation experiments we attempt to control the experiment a little better for the sake of the experimentalist, as well as to improve the analysis and interpretation of the results. A typical deformation apparatus is schematically shown in Figure 10.5a.

FIGURE 10.5. Schematic diagram of (a) a triaxial compression apparatus and (b) states of stress in cylindrical specimens in compression and extension tests. The values of Pc, Pf, and σ can be varied during the experiments. [5.8]

In this rig, a cylindrical rock specimen is placed in a pressure chamber, which is surrounded by a pressurized fluid that provides the confining pressure, Pc, on the specimen through an impermeable jacket. This experimental setup is known as a triaxial testing apparatus, named for the triaxial state of the applied stress, in which all three principal stresses are unequal to zero. For practical reasons, two of the principal stresses are equal. In addition to the fluid that provides the confining pressure, a second fluid may be present in the specimen to provide pore-fluid pressure, Pf. The difference between confining and pore pressure, Pc – Pf, is called the effective pressure (Pe). Adjusting the piston at the end of the test cylinder results in a maximum or minimum stress along the cylinder axis, depending on the magnitudes of fluid pressure and axial stresses. The remaining two principal stresses are equal to the effective pressure. By varying any or all of the axial stress, the confining pressure, or the pore-fluid pressure, we obtain a range of stress conditions to carry out our deformation experiments (Figure 10.5b). In addition to stress and pressure, we can heat the sample during the experiment to examine the effect of temperature. This rig configuration allows a limited range of finite strains, so a torsion rig with rotating plates is used for experiments at high shear strains.

A triaxial apparatus enables us to vary stress, strain, and strain rate in rock specimens under carefully controlled parameters of confining pressure, temperature, pore-fluid pressure, and time (that is, duration of the experiment). What happens when we vary these parameters and what does this tell us about the behavior of natural rocks? Before we dive into these experiments we briefly review how these environmental properties relate to the Earth.

FIGURE 10.6. Temperature (T) and pressure (Pc) with depth. The dashed line is the adiabatic gradient, which is the increase of temperature with depth resulting from increasing pressure and the compressibility of silicates. Approximate boundaries of crust and mantle, and lithosphere (Li) and asthenosphere (As) are marked. [5.9]

Both confining pressure and temperature increase with depth in the Earth (Figure 10.6). As we saw earlier, the confining pressure is obtained from the depth-dependent relationship, Pc = ρ ⋅ g ⋅ h, where ρ is the density, g is gravity, and h is depth. Since this pressure is the weight of the overlying rock column, we call it the lithostatic pressure. The temperature structure of the Earth is slightly more complex than the constant gradient of 10oC K/km used earlier. At first, temperature increases at an approximately constant rate (10°C/km–30°C/km), but then the thermal gradient is considerably less (Figure 10.6). Additional complexity is introduced by the heat generated from compression at high pressures, which is reflected in the adiabatic gradient (dashed line in Figure 10.6). But if we limit our considerations to the crust and uppermost mantle, a linear geothermal gradient in the range of 10°C/km–30°C/km is a reasonable approximation.

Earlier we learned that tectonic processes occur at strain rates on the order of 10-12-10–15/s, with the exception of meteoric impacts, seismic events, and explosive volcanism. In contrast to tectonic strain rates, experimental work is typically limited by the patience and the life expectancy of the experimentalist. Some of the slowest laboratory experiments are carried out at strain rates of 10–8/s (i.e., 30% shortening in a year), which is four to seven orders of magnitude greater than geologic rates. With these caveats we look at the effects on rock of varying environmental conditions during deformation experiments.

Confining Pressure

You recall from Chapter 3 that confining pressure acts equally in all directions, so it imposes an isotropic stress on the specimen. When we change the confining pressure during our experiments we observe a very important characteristic: increasing confining pressure results in greater strain accumulation before failure. In other words, increasing confining pressure increases the viscous component and therefore the rock’s ability to flow. What is the explanation for this? The Mohr circle for stress and failure criteria provided an earlier explanation, so instead we’ll use an analog. Moving your arm as part of a workout exercise is quite easy, but executing the same motion under water is a lot harder. Water “pushes” back more than air does, and in doing so it resists the motion of your arms. Similarly, higher confining pressures resist the opening of rock fractures, so any shape change that occurs is therefore viscous (ignoring the small elastic component).

(a)

(b)

FIGURE 10.7. (a) Compression stress–strain curves of limestone at various confining pressures (indicated in MPa) at 400°C. (b) The effect of changing the confining pressure on various rock types. Among common rocks, the amount of strain before failure (ductility) varies significantly. [5.10/11]

The effect of confining pressure is particularly evident at elevated temperatures, where fracturing is increasingly suppressed (Figure 10.7a). When we compare common rock types, the role of confining pressure varies considerably (Figure 10.7b); for example, the effect is much more pronounced in sandstone and shale than in quartzite and slate. Thus, we learn that larger strains can be achieved with increasing depth in the Earth, where we find higher lithostatic pressures.

Temperature

A change in temperature conditions produces a marked change in behavior. Using the same limestone as in the confining pressure experiments above, we find that the material fails rapidly at low temperatures (Figure 10.8). Moreover, under these conditions most of the strain prior to failure is recoverable (elastic).


FIGURE 10.8. (a) Compression stress–strain curves of limestone at various temperatures (indicated in °C) at 40 MPa confining pressure. (b) The effect of temperature changes on the compressive strength of some rocks and minerals. [5.12/13]

When we increase the temperature, the elastic portion of the strain decreases, while the ductility increases, which is most noticeable at elevated confining pressures. You experience this temperature dependence of flow also if you pour syrup on pancakes in a tent in the Arctic or in the Sahara: the ability of syrup to flow increases with temperature. Furthermore, the maximum stress that a rock can support until it flows (called the yield strength of a material) decreases with increasing temperature. The behavior of various rock types and minerals under conditions of increasing temperature is shown in Figure 10.8b, from which we see that calcite-bearing rocks are much more affected than, say, quartz-bearing rocks. Collectively these experiments demonstrate that rocks have lower strength and are more ductile with increasing depth in the Earth, where we find higher temperatures.

Pore-Fluid Pressure

Natural rocks commonly contain a fluid phase that may originate from the depositional history or may be secondary in origin (for example, fluids released from prograde metamorphic reactions). In particular, low-grade sedimentary rocks such as sandstones and shales, contain a significant fluid component that will affect their behavior under stress. To examine this parameter, the deformation rig contains an impermeable jacket around the sample. Experiments show that increasing the pore-fluid pressure produces a drop in the sample’s strength and reduces its ductility (Figure 10.9a). In other words, rocks are weaker when the pore-fluid pressure is high.

(c)

FIGURE 10.9. Comparing the effect on the behavior of limestone of (a) varying pore-fluid pressure and (b) varying confining pressure. (c) The effect of water content on the behavior of natural quartz. Dry and wet refer to low and high water content, respectively. The curves also reflect the effect of temperature on deformation. [5.16/17]

Pore-fluid pressure acts equally in all directions and thus counteracts the confining pressure, resulting in an effective pressure (Pe = Pc – Pf) that is less than the confining pressure. Thus, we can hypothesize that increasing the pore-fluid pressure has the same effect as decreasing the confining pressure of the experiment. We put this to the test by comparing the result of two experiments on limestone in Figure 10.9a and 10.9b that vary pore-fluid pressure and confining pressure, respectively. Clearly, there is remarkable agreement between the two experiments, supporting our hypothesis.

The role of fluid content is a little more complex than is immediately apparent from these experiments, because of fluid-chemical effects. While ductility decreases with increasing pore-fluid pressure, the corresponding decreased strength of the material will actually promote flow. The same material with low fluid content (“dry” conditions) would resist deformation, but at high fluid content (“wet” conditions) flow occurs readily. This is nicely illustrated by looking at the deformation of quartz with varying water content (Figure 10.9c). The behavior of quartz is similar to that in the previous rock experiment: the strength of “wet” quartz is only about one tenth that of “dry” quartz at the same temperature. The reason for this weakening lies in the substitution of OH groups for O in the silicate crystal lattice, which strains and weakens the Si-O atomic bonds; this is called hydrolytic weakening. In practice, fluid content explains why most minerals and rocks deform readily even under moderate stress conditions.

Strain Rate

It is impossible to carry out rock deformation experiments at geologic rates, so it is particularly important for the interpretation of experimental results to understand the role of strain rate. The effect is clearly seen in experiments at elevated temperatures, such as those on marble (Figure 10.10).

(a)

(b)

FIGURE 10.10 Stress versus strain curves for extension experiments in weakly foliated Yule marble for various constant strain rates at 500°C. (b) Log stress versus –log strain rate for various temperatures based on extension experiments in Yule marble. The heavy lines mark the range of experimental data; the thinner part of each curve extrapolates to smaller strain rates. Tectonic strain rates are marked by the blue box. [5.14/15]

Decreasing the strain rate results in decreased rock strength and increased ductility. We again turn to an analogy for our understanding. If you slowly press a hammer on a small ball of Silly Putty® it spreads under the applied stress (ductile flow). If, on the other hand, you deform that ball by a more rapid blow of the hammer, the material will shatter into many pieces (that is, brittle failure). Although the environmental conditions are the same, the response is dramatically different because the strain rate differs.

Because rocks show similar effects from strain rate variation, the Silly Putty® experiment highlights a great uncertainty in experimental rock deformation. Extrapolating experimental results for strain rates over many orders of magnitude has significant consequences (Figure 10.10b). Consider a strain rate of 2x10–‑14/s and a temperature of 500°C, where ductile flow occurs at a differential stress of 10 MPa. At the same temperature, but at an experimental strain rate of 10‑6/s, the flow stresses are nearly an order of magnitude greater (160 MPa). Comparing this with the results of temperature experiments, you will notice that temperature change produces effects similar to strain rate variation in rock experiments (higher t ∝ lower ė); temperature is therefore used as a substitute for geologic strain rates. In spite of these uncertainties, the volume of experimental work and our understanding of the mechanisms of flow allow us to make reliable extrapolations from rock deformation to deformation at tectonic strain rates.

Strain-dependent Behavior

The rock experiments bring a key property to light that we earlier noticed in the general creep curve, namely, that the relationship between strain and time varies within a single experiment. The strain rate may decrease, increase, or remain constant under constant stress. When we carry out experiments at a constant strain rate we often find that the stresses necessary to continue the deformation may increase or decrease, phenomena that engineers call work hardening (greater stress needed) and work softening (lower stress needed), respectively. In a way you can think of this as the rock becoming stronger or weaker with increasing strain; therefore, we can also call the effects strain hardening and strain softening, respectively.

A well-known application of work hardening is the repeated rolling of metal that gives it greater strength, especially when it is heated. While you may not realize this from the repair bill after an unfortunate encounter with a moving tree, car makers use work hardening to strengthen metal parts. This effect was already discovered in ancient times, when Japanese samurai sword makers were producing some of the hardest blades available using repeated heating and hammering of the metal. Work softening is the opposite effect, in which the stress required to continue the experiment is less; in constant stress experiments this results in a strain rate increase. Both processes can occur in the same material, where, at low confining pressure a stress drop is observed. At high confining pressures, the material work hardens, requiring increasingly higher stresses to continue the experiment.

FIGURE 10.11. Representative stress–strain curves of brittle (A and B), brittle-plastic (C), and

plastic behavior (D–F). A shows elastic behavior followed immediately by failure. In B, a small viscous component (permanent strain) is present before failure. In C, a considerable amount of permanent strain accumulates before the material fails. D illustrates work softening; E represents ideal elastic-plastic behavior, in which permanent strain accumulates at constant stress above the yield stress. F shows the behavior in many of the earlier experiments, with a component of elastic strain followed by permanent strain that requires increasingly higher stresses to accumulate (work hardening). The yield stress marks the stress at the change from elastic (recoverable or non-permanent strain) to viscous (non-recoverable or permanent strain) behavior; failure stress is the stress at fracturing. [5.18]

These behaviors are schematically summarized in Figure 10.11, where curve D displays work softening and curve F is work hardening. Work hardening and softening reflect atomic-scale processes that enable rocks to deform plastically.

Competency and Strength

We already introduced the term strength in our discussion, which is the stress that a material can support before permanent deformation (Figure 10.11). Competency is a relative term that compares the resistance of rocks to deformation. The laboratory experiments discussed earlier support our general field observations of a qualitative competency scale for rocks. The competency of sedimentary rocks increases in the order:

rock salt → shale → limestone → greywacke → sandstone → dolomite.

For metamorphic/igneous rocks the order of increasing competency is:

schist → marble → quartzite → gneiss → granite → basalt.

Note that competency is not the same as the amount of strain that accumulates in a body, so ductility should not be used as a synonym for competency.

Synthesis: From Laboratory to Nature

We close this section on experiments with a summary table that incorporates the results of varying the confining pressure, temperature, fluid pressure, and strain rate in experiments on rocks, and by examining the significance for geologic conditions.

	Effect	Explanation
High Pc	Suppresses fracturing; increases ductility; increases strength; increases work hardening	Prohibits fracturing and frictional sliding; higher stress necessary for fracturing exceeds that for ductile flow
High T	Decreases elastic component; suppresses fracturing; increases ductility; reduces strength; decreases work hardening	Promotes crystal plastic processes
High Pf	Decreases elastic component; promotes fracturing; reduces ductility; reduces strength or promotes flow	Decreases Pc (Pe = Pc – Pf) and weakens Si-O atomic bonds
Low ė	Decreases elastic component; increases ductility; reduces strength; decreases work hardening	Promotes crystal plastic processes

From the Table we see that increasing confining pressure (Pc) and fluid pressure (P) have opposing effects, while increasing temperature (T) and lowering strain rate (ė) have the same effect. Confining pressure and temperature, which both increase with depth in the Earth, increasingly resists failure, while promoting larger strain accumulation; that is, they increase the ability of rocks to flow. High pore-fluid content is more complicated as it favors fracturing if Pf is high or promotes flow in the case of intra-crystalline fluids. From these observations we predict that brittle behavior (fracturing) is largely restricted to the upper crust, while plastic behavior (flow) dominates at depth. Natural occurrences supporting this prediction is the realization that faulting and earthquakes generally occur at shallow crustal levels (<15 km depth), while large-scale material flow dominates the deeper crust and mantle.

A MICROSTRUCTURAL VIEW OF LABORATORY BEHAVIOR

While our exploration thus far has been mostly observational and descriptive, understanding the mechanisms that support the various behaviors return us to the realm of crystal structures. To recap, rock deformation experiments typically show the same sequence where, after an initial elastic stage, permanent strain accumulates. The elastic component is recoverable and does not involve crystal plastic processes, but the permanent strain component is primarily achieved by the motion of defects.

Steady-state flow, strain accumulation at constant stress and strain rate, requires that the generation, motion and annihilation of dislocations is sufficiently fast to occur at a constant rate of strain. But what explains, for example, work hardening, where material requires an increasingly larger stress to deform? We can safely assume that the ancient samurai makers did not know that dislocations are responsible for their strong sword’s property. Inefficient climb and cross-slip at low temperatures prevent dislocations from slipping past inclusions and other obstacles, thus limiting plastic flow. Adding decreased dislocation annihilation, this causes dislocation density in a crystal to increase, which further affects the ability of dislocations to glide, as they interact with one another. Recall that the ability of dislocations to glide produces strain, so dislocation tangles restrict motion and, thus, the rate of strain accumulation decreases (unless the stress is increased). With so many dislocations in a crystal, the chance of interaction is large, so let’s look at this in a little more detail to get a fuller appreciation of the importance of defects.

FIGURE 10.12. The formation of a jog from the interaction of two mobile edge dislocations. For simplicity, dislocation D2 is initially kept stationary while dislocation D1 moves; the glide planes (shaded and unshaded), Burgers vectors (b), and dislocation lines (l) for each edge dislocation are shown (a). As D1 passes through dislocation line l2, a small step of one Burgers vector (b1) length is created; this small step is a jog, with a differently oriented dislocation line segment but the same b2 (b). As a consequence, the glide plane, containing l2 and b2, is different along l2. In fact, the glide plane of the jog is the same as that for D1, but with a different Burgers vector. Assuming that the CRSS for glide differs in different directions, the ability for D2 to move is no longer the same along l2, and the jog pins the dislocation by anchoring a segment of l2 (c). [9.22]

Figure 10.12 shows a situation where an edge dislocation (D1) moves relative to another edge dislocation (D2) with a different slip planes (we keep dislocation D2 stationary for convenience of illustration). As D1 passes through D2, the dislocation line l2 is offset. This offset, called a jog, has an important implication. Whereas the Burgers vector b2 for dislocation D2 remains the same along the dislocation line, its glide plane has changed at the jog. Motion of dislocation D2 requires a critical resolved shear stress (CRSS) for glide on the initial slip plane, but it also needs movement on a second slip plane for that dislocation. Because the values of the CRSS differ for crystal planes in different orientations, the ability for glide will vary along the dislocation line when a jog is present, resulting in a dislocation that is held back, or pinned, at the jog (Figure 10.12). Pinning reduces the motion of a dislocation which causes the material to strengthen, expressed as work hardening in experiments. Diffusion of vacancies can overcome this restriction, so work hardening is much less important in the high-temperature regime. In summary, impurities that pin dislocations or high dislocation densities that restrict motion (tangles) result in work hardening of materials, which is overcome by the activity of higher-temperature dislocation climb. Work softening is also observed occurs, which can similarly be explained by adding the effect of grain-size reduction in plastically-deforming materials.

NON-LINEAR RHEOLOGY

A fundamental characteristic of rheologic models of the lithosphere so far is a linear relationship between strain rate and stress: ė ∝ σ. Experiments on geologic materials (like silicates) at elevated temperature show, however, that the relationship between strain rate and stress is often non-linear (Figure 10.13), with: ė ∝ σn; where the exponent n is greater than 1.

FIGURE 10.13. Linear (a) and non-linear rheologies (b) in a stress–strain rate plot. The viscosity (η) is defined by the slope of the linear viscous line in (a) and the effective viscosity (ηe) by the slope of the tangent to the curve in (b). [5.5]

In other words, the proportionality of strain rate and stress is not constant. Rather, strain rate changes as a function of stress, and vice versa. This behavior is also displayed by wet paint, which therefore serves as a suitable analog. A physical model representative of rocks showing nonlinear behavior is shown in Figure 10.14, and is known as elastic-plastic behavior.

FIGURE 10.14. Elastic-plastic behavior. (a) A physical model consisting of a block and a spring; the associated strain–time curve (b) and stress–strain rate curve (c). Compare the strain-time curves of Figure 5.6b and 5.2a. [5.6]

In this configuration a block and a spring are placed in series. The spring extends when a stress is applied, but only elastic (recoverable) strain accumulates until a critical stress is reached (the yield stress), above which the block moves and permanent strain occurs. The yield stress has to overcome the resistance of the block to moving (friction), but, once it moves, the stress remains constant while the strain accumulates. In fact, you experience elastic-plastic behavior when towing your car with a nylon rope that allows some stretch. Removing the elastic component (e.g., a sliding block with a non-elastic rope) is called ideal plastic behavior.

Effective viscosity and Strength

An important consequence of non-linear rheologies is that we can no longer talk about (Newtonian) viscosity, because, as the slope of the stress–strain rate curve changes, the viscosity also changes. Nevertheless, as it is convenient for modeling purposes to use viscosity at individual points along the curve, so we define the effective viscosity (ηe) as:

ηe = σ/ė Eq. 10.4

This relationship is the same as that for viscous behavior, but in the case of effective viscosity you have to remember that ηe changes as the stress and/or the strain rate change. In Figure 10.14 you see that the effective viscosity (the tangent of the slope) decreases with increasing stress and strain rate, which means that flow proceeds faster under these conditions. Thus, effective viscosity is not a material property like Newtonian viscosity, but a convenient description of behavior under known conditions of stress (or strain rate). For this reason, ηe is also called stress-dependent viscosity or strain rate–dependent viscosity.

The constitutive equation describing the relationship between strain rate and stress for non-linear behavior is:

ė = A . σn . exp(–E*/RT) Eq. 10.5

where E* is the activation energy, is an empirically derived value that is typically in the range of 100–500 kJ/mol, and n, the stress exponent, in the range 1 > n > 5 for most natural rocks, with n = 3 a representative value. Crystal plasticity is temperature dependent and requires a minimum energy to occur, which is included in the exponential part of the function as the activation energy (E*) and temperature (T in Kelvin); A is a constant, and R is the gas constant [Remember that exp(a) means ea, with e = 2.72]. Values for A, n, and E* are experimentally derived and listed in Supporting Material. Assuming a constant strain rate, we can solve the equation for various temperatures.

First, we rewrite Equation 10.5 as a function of stress:

σ = (ė/A)1/n . exp(E*/nRT) Eq. 10.6

Substituting the relevant values for A, n, and E* at constant T for different rock types, we find that the flow stress for rock salt is much less than that for any other rock types. This fits the observation in the opening chapter that rock salt flows readily at near-surface conditions. Limestones, shales and marbles are also relatively weak and, therefore, regional deformation is often localized in these rocks. Quartz-rich rocks, such as quartzites and granites, in turn, are weaker than plagioclase-bearing rocks. Olivine-bearing rocks are among the strongest of rock types, meaning that they require large differential stresses to flow. This led to the mistaken view of the pre-1960s that the deep Earth is mechanically strong.

FIGURE 10.15. Strength as a function of temperature (=depth) for common rock types, using a geothermal gradient of 10 K/km and a strain rate of 10‑14/s. The relative location of frictional behavior is added (brown). Rs = rock salt, Gr = granite, Gr(w) = wet granite, Qz = quartzite, Qz(w) = wet quartzite, Pg = plagioclase-rich rock, QzD = quartz diorite, Db = diabase, Ol = Olivine-rich rock. [5.7]

Instead, how can Earth’s mantle flow when we only have differential stresses on the order of tens of megapascals? The answer is obtained by solving Equation 10.6 for various temperatures. In Figure 10.15 this is done using a “cold” geothermal gradient of 10 K/km for key rock types [Note: A representative “hot” geothermal gradient would be 30 K/km]. The graph illustrates our first-order conclusion on the relative strength of various rock types, but also shows that, with increasing temperature (=depth), the strength of rock types decreases significantly. The latter is an important observation for understanding the nature of deformation processes in the deep Earth and the properties of the lithosphere.

EARTH’S RHEOLOGIC LAYERING

In the early part of the twentieth century, long before the acceptance of plate tectonics, geologists noticed that the thickness of the crust was not uniform, and that, where crust was thicker, its top surface lay at higher elevations (Figure 10.16).

FIGURE 10.16. Schematic cross section of the lithosphere illustrating characteristic variations in crust, mantle and lithospheric thicknesses. [14.10]

This behavior reminded geologists of a classic bathtub experiment in which wood blocks of different thickness were placed in water—the surface of the thicker blocks lay at a higher elevation than the surface of thinner blocks. Could the crust (or the crust together with the topmost layer of mantle) be “floating” on a weaker layer of mantle below? If so, then the mantle, below a certain depth, would have to be able to respond to stress by flowing. Geologists also noticed that when a large glacier grew on the surface of the Earth, it pushed the surface of the Earth down, creating a broad dimple that was wider than the load itself. To picture this dimple, imagine the shape of the indentation that you make when you stand on the surface of a trampoline or a mattress. Could the outermost layer of the Earth respond to loads by flexing, like a stiff sheet of rubber?

FIGURE 10.17. Comparison of seismic layering and rheologic layering of Earth. Note that the relative strong lithosphere consists of the crust and uppermost mantle. [14.10]

To explain the above phenomena, geologists realized that we needed to look at earth layering, at least for the outermost several hundred kilometers, by considering the way layers respond to applied stress. In other words, we had to consider rheologic layering (Figure 10.17). By doing this, we divide the outer several hundred kilometers into two layers based on the way that layers respond to stress. This perspective contrasts that provided by studying lithologies and seismic discontinuities in Earth.

We refer to the outer, relatively rigid shell of the Earth that responds to stress by bending or flexing, as the lithosphere. The lithosphere, which consists of the crust and outermost mantle, overlies an interval of the mantle that responds to stress by plastically flowing. This weak layer is called the asthenosphere. When plate tectonics theory came along in the 1960s, it proved convenient to picture the tectonic plates as large pieces of lithosphere. In fact the term “lithospheric plate” has become standard geologic jargon. The plates move over the asthenosphere because it is comparatively weak. Some work suggests that ancient continental plates have roots that extend down into the asthenosphere. Asthenosphere, perhaps down to a depth of 250 km, moves with the continental lithosphere as the tectonic plate moves. This thicker entity, lithosphere plus coupled upper asthenosphere, has been called the tectosphere. For our discussion we consider that tectonic plates are composed of only lithosphere.

Strength Profiles

Armed with information on lithologic responses to changes in environmental conditions and knowledge of the dominant lithologies with depth, we can determine first-order strength properties from a combination of non-linear rheologies and frictional properties. Recall that, for a given strain rate, behavior in the frictional regime is mostly a function of stress, represented by the frictional strength line. Deformation in the plastic regime is mostly sensitive to temperature and lithology, represented by non-linear rheologies above. Using representative, mono-mineralic lithologies, with a quartz-dominated upper crust, a feldspar-dominated lower crust and an olivine-dominated upper mantle, we obtain a composite strength profile (Figure 10.18). The dominance of friction over plastic flow is defined by which deformation mechanisms is most efficient at a given differential stress and tectonic strain rate.

Figure 10.18. (a) Stratification of the lithosphere based on the frictional and plastic properties of characteristic minerals. (b) Composite lithospheric strength (differential stress) curve changes as a function of composition and depth (=temperature) in Earth.

Composite strength curves for the mantle and crust link the role of compositional stratification and mechanical behavior. These diagrams provide first-order predictions of Earth rheology that are in numerical models toward more advanced study of lithosphere dynamics.

The Lithosphere

The lithosphere, derived from the Greek word lithos for rock (implying that it has strength, or resistance to stress), is the uppermost rheologic layer of Earth. As noted above, lithosphere consists of the crust and the uppermost (coolest and strongest) mantle; the mantle part of the lithosphere is called the lithospheric mantle. As we’ve noted already, the lithosphere can be distinguished rheologically from the underlying layer, the asthenosphere, because, overall, the lithosphere behaves rigidly on geologic timescales. If you place a load on it, the lithosphere either supports the load or bends—it does not simply flow out of the way. In technical terms, we say that lithosphere has flexural rigidity.

FIGURE 10.19. A sheet of rubber has flexural rigidity and bends when a load is placed on it. In contrast, the underlying honey flows out of the way. [14.11]

To picture what we mean by flexural rigidity, imagine a stiff rubber sheet resting on a layer of honey (Figure 10.19). The sheet has flexural rigidity, so if you place an empty can (a small load) on the sheet, the sheet supports it, and if you place a concrete block (a large load) on the sheet, the sheet bends. If we were to do the same experiment with a material that does not have flexural rigidity, the results would be different. For example, if we place a can directly on the surface of a pool of honey, a material without flexural rigidity, the can sinks in a little and then floats, while if we place the concrete block in the honey, the block sinks. The honey is able to flow out of the way of the block as the block sinks and can then flow over the top of the block as the block passes. In sum, flexural rigidity is the resistance to bending (flexure) of a material. A steel beam has a relatively high flexural rigidity, but a sheet of rubber has low flexural rigidity. Non-elastic materials, like honey or lava, have no flexural rigidity at all. Not all lithosphere on the Earth has the same flexural rigidity. Old, cold cratons have greater flexural rigidity than younger and warmer orogens.

Significantly, the rheologic behavior of the lithosphere affects the way in which heat can be transported through it. Because the lithosphere cannot flow easily, heat moves through the lithosphere only by conduction or advection, not by convection. In contrast, as we see later, heat is transported in the asthenosphere primarily by convection.

As noted above, the lithosphere includes all of the crust and the uppermost part of the mantle. For simplicity, the base of the lithosphere can be defined by an isotherm, meaning an imaginary surface on which all points have the same temperature. Geologists often define the 1280°C isotherm in the mantle as the base of the lithosphere, because at approximately this temperature, olivine, the dominant silicate mineral in mantle rocks, becomes very weak; this weakness happens because dislocation creep and diffusional processes become very efficient at these temperatures. In other words, we view the boundary between the lithosphere and underlying asthenosphere as a thermal boundary. In contrast, the boundary between the crust and the upper mantle (which collectively make up the lithosphere) is a compositional boundary, meaning it is due to a change in chemical makeup.

The depth of the 1280° C isotherm is not fixed in the Earth, but varies depending on the thermal structure of the underlying mantle and on the duration of time that the overlying lithosphere has had to cool. Thus, the base of the lithosphere is not at a fixed depth everywhere around the Earth (Figure 10.17). Moreover, at a given location, the depth of the base of the lithosphere can change with time if the region is heated or cooled. For example, directly beneath the axis of ocean ridges, the lithosphere is very thin, because the 1280° C isotherm rises almost to the base of newly-formed crust. Yet beneath the oceanic abyssal plains, oceanic lithosphere is older and has had time to cool; here it reaches a thickness of about 100 km. As a result, the lithospheric mantle of an oceanic plate thickens with time as seafloor spreading occurs, and the plate moves away from an ocean ridge. Beneath continental cratons, the lithosphere is very old and may be more than 150 km thick.

The Asthenosphere

The asthenosphere, derived from the Greek asthenes, meaning without strength, is the layer of mantle that underlies the lithosphere. Because the asthenosphere is warm and highly plastic, it behaves close to a viscous fluid, which does not have flexural rigidity over geologic time scales. Remember that we saw earlier that, over very short timescales, the mantle can behaves elastically, as it transmits seismic waves. Thus, if a negatively buoyant load is placed on the asthenosphere, it sinks as the asthenosphere flows away from the heavier load (Figure 10.20).

FIGURE 10.20. A load placed in a material with no flexural rigidity sinks into it, if the load has negative buoyancy. [14.11]

Because the asthenosphere has no flexural rigidity, lateral density differences that result from variations in temperature and/or composition cause the asthenosphere to flow. Specifically, warmer and less dense parts of the asthenosphere rise, while denser parts sink; in other words, heat transfer in the asthenosphere occurs by convection. Keep in mind that even though the asthenosphere is able to flow, it is almost entirely composed of solid rock; its mechanical behavior should not be viewed as a subterranean sea of magma. Indeed, the only magma in the asthenosphere occurs either in the low-velocity zone, where a slight amount of melt is found as films on the surface of grains, or in regions beneath large volcanic provinces, where blobs of magma accumulate and rise. In Supplementary Materials we further explore the effect of buoyancy under the topic isostasy.

As we’ve mentioned above, the top of the asthenosphere can be defined approximately by the 1280° C isotherm, for above this thermal boundary, peridotite is cool enough to behave rigidly, while below this boundary, peridotite is warm enough to behave more plastically. However, there is no significant contrast in chemical composition across this boundary. Defining the base of the asthenosphere is a matter of semantics, because all mantle below the lithosphere is soft enough to flow plastically. Some geoscientists consider the asthenosphere to be equivalent to the seismologic low-velocity zone in the upper portion of the upper mantle. Others, equate it with the interval of mantle between the base of the lithosphere and the top of the transition zone. Still others equate it with the interval between the base of the lithosphere and the top of the lower mantle, where earthquakes no longer occur, or even with all the mantle below the lithosphere. There really isn’t consensus on this issue.

Back to The Lithosphere Contents

Back to PSG&T Home

v1.3 Last update: 15-Sep-2023

[1] after the Irish physicist William Kelvin (1824–1907).

[2] after the Scottish physicist James C. Maxwell (1831–1879).