The geologic history of most crustal rocks involves significant changes in the shape of original features like sedimentary bedding, igneous structures, rock inclusions, and grains. The formation of folds or faults springs to mind as an example of this deformation, which we examine in detail later in the book. A small-scale example of deformation is illustrated in the slab of rock in Figure 6.1, which contains Cambrian trilobites that were distorted from the original shape of these fossils. Deformed fossils, folds, and other features document the permanent shape changes that occur in natural rocks. The study and quantification of these distortions, which occur in response to forces acting on bodies, is the subject of this chapter.

FIGURE 6.1. Deformed trilobites in Cambrian slate from Wales, UK. Knowledge about their original symmetry enables us to quantify the strain in these rocks. [4.1]

Recall the force of gravity, for example. Pouring syrup on pancakes is easy because of Earth’s gravity, but in a space station it is quite difficult to keep the syrup in its preferred place. That you are able to read this text sitting down is another convenient effect of Earth’s gravity; in a space station you would be floating around (possibly covered by syrup). Let us consider a more controlled experiment to analyze the response of materials to an applied force. We can change the shape of a block of clay or silly putty by the action of, say, your hands or a vise. When forces affect the spatial geometry of a body (syrup, you, rocks) we enter the realm of deformation. Most simply stated: deformation of a body occurs in response to forces. We will see later that deformation affects stress (force acting on an area), so there is no simple stress–deformation relationship. The response of a body to forces may have many faces. In some cases, the body is merely displaced or rotated, such as when you get up from the chair and move around the room. In other cases, the body becomes distorted, as in the clay block experiment or with the flow of syrup. In this chapter we will examine these responses both qualitatively and quantitatively.

DEFORMATION AND STRAIN

Deformation and strain are closely related terms that are sometimes used as synonyms, but they are not the same. Deformation describes the collective displacements of points in a body; in other words, it describes the complete transformation from the initial to the final geometry of a body. This change can include a translation (movement from one place to the other), a rotation (spin around an axis), and a distortion (change in shape). Strain describes the changes of points in a body relative to each other; so, it describes the distortion of a body. This distinction between deformation and strain may not be immediately obvious from these abstract descriptions, so we use an example. In Figure 6.2 we change the shape and position of a square, say, a slice of the clay cube we used in Chapter 3. We arbitrarily choose a reference frame with axes that parallel the margins of the printed page. The displacement of points within the body, represented by the four corner points of the square, are indicated by vectors. These vectors describe the displacement field of the body from the initial to the final shape.

The displacement field is subdivided into three components:

A distortion (Figure 6.2b)
A rotation (Figure 6.2c)
A translation (Figure 6.2d)

FIGURE 6.2. The components of deformation. The deformation of a square (a) is subdivided into three independent components: (b) a distortion; (c) a rotation; and (d) a translation. The displacement of each material point in the square, represented by the four corners of the initial square, describes the displacement field. The corresponding strain ellipse is also shown. The distortion occurs along the axes X and Y, which are the principal strain axes. [4.2]

Each component in turn can be described by a vector field (shown for point A only) and their sum gives the total displacement field. Importantly, a change in the order of addition of these vector components affects the final result. Deformation, therefore, is not a vector entity, but a second-order tensor (similar to stress). We will return to this later.

When the rotation and distortion components are zero, we only have a translation. This translation is formally called rigid-body translation (RBT), because the body undergoes no shape change while it moves. For convenience, we will simply refer to this component as translation, and the deformation is called translational. When the translation and distortion components are zero, we have only rotation of the body. By analogy to translation, we call this component rigid-body rotation (RBR), or simply spin, and the corresponding deformation is called rotational. Recalling the pool table example of Chapter 2, the deformation of a pool ball that is hit is fully described by a translational and a spin component. When translation and spin are both zero, the body undergoes distortion; this component is described by strain. So, strain is a component of deformation and therefore not a synonym. In essence, we have defined deformation and strain relative to a frame of reference. Deformation describes the complete displacement field of points in a body relative to an external reference frame, such as the edges of the paper on which Figure 6.2 is drawn. Strain, on the other hand, describes the displacement field of points relative to each other. This requires a reference frame within the body, an internal reference frame, like the edges of the square. Place yourself in the square and you would be unaware of any translation, just as when you are flying in an airplane or riding a train. Looking out of the window, however, makes you aware of the displacement by offering an external reference frame.

One final element is missing in our description of deformation. In Figure 6.2 we have constrained the shape change of the square by maintaining a constant area. You recall that shape change results from the deviatoric component of the stress, meaning where the principal stresses are unequal in magnitude (see Chapter 2). The hydrostatic component of the total stress, however, contributes to deformation by changing the area (or volume, in three dimensions) of an object. Area or volume change is called dilation and is positive or negative, as the volume increases or decreases, respectively. Because dilation results in changes of line lengths it is similar to strain, except that the relative lengths of the lines remain the same. Thus, it is useful to distinguish strain from volume change.

In summary, deformation is described by:

Rigid-body translation (or translation)
Rigid-body rotation (or spin)
Strain
Volume change (or dilation)

It is relatively difficult in practice to determine the translational, spin, and dilational components of deformation. Only in cases where we are certain about the original position of a body can translation and spin be determined, and only when we know the original volume of a body can dilation be quantified. On the other hand, we often do know the original shape of a body, so the quantification of strain is a common activity in structural geology.

HOMOGENEOUS STRAIN AND STRAIN ELLIPSE

Strain describes the distortion of a body in response to an applied force. Strain is homogeneous when any two portions of the body that were similar in form and orientation before are similar in form and orientation after strain. This can be illustrated by drawing a square and a circle on the edge of a deck of cards; homogeneous strain changes a square into a parallelogram and a circle into an ellipse (Figure 6.3). We define homogeneous strain by its geometric consequences:

Originally straight lines remain straight.
Originally parallel lines remain parallel.
Circles become ellipses; in three dimensions, spheres become ellipsoids.

FIGURE 6.3. Homogeneous and heterogeneous strain. A square and a circle drawn on a stack of cards (a) transform into a parallelogram and an ellipse when each card slides the same amount, which represents homogeneous strain (b).

Heterogeneous strain (c) is produced by variable slip on the cards, for example by increasing the slip on individual cards from bottom to top. [4.3]

When one or more of these three restrictions does not apply, we call the strain heterogeneous (Figure 6.3c). Because conditions (1) and (2) are maintained during the deformation components of translation and rotation, deformation is homogeneous by definition if the strain is homogeneous. Conversely, heterogeneous strain implies heterogeneous deformation. Homogeneous and heterogeneous deformation should not be confused with rotational and nonrotational deformation; the latter reflects the presence of a spin component.

Because heterogeneous strain is more complex to describe than homogeneous strain, we try to analyze heterogeneously strained bodies or regions by separating them into homogeneous portions. In other words, homogeneity of deformation is a matter of scale. Consider a heterogeneous deformation feature like a fold, which can be approximated by three essentially homogeneous sections: the two limbs and the hinge (see Chapter 10 for fold terminology). The heterogeneously deformed large square of Figure 6.3c consists of nine smaller squares for which the strain conditions are approximately homogeneous. Given the scale dependence of homogeneity and not to complicate our explanations unnecessarily, we will limit our discussion in this chapter to homogeneous strain.

FIGURE 6.4. Homogeneous strain describes the transformation of a square to a rectangle, or a circle to an ellipse. Two material lines that remain perpendicular before and after strain (red lines) are the principal axes of the strain ellipse (X and Y). Dashed lines are material lines that do not remain perpendicular after strain; they rotate toward the long axis (X) of the strain ellipse. [4.4]

In a homogeneously strained, two-dimensional body there will be at least two material lines that do not rotate relative to each other, meaning that their angle remains the same before and after strain. What is a material line? A material line connects features, such as an array of grains, that are recognizable throughout a body’s strain history. The behavior of four material lines is illustrated in Figure 6.4 for the two-dimensional case, in which a circle changes into an ellipse. In homogeneous strain, two orientations of material lines remain perpendicular before and after strain. These two material lines form the axes of an ellipse that is called the strain ellipse. Note that the lengths of these two material lines change from the initial to the final stage; otherwise we would not strain our initial circle. Analogously, in three dimensions we have three material lines that remain perpendicular after strain and they define the axes of an ellipsoid, the strain ellipsoid. The lines that are perpendicular before and after strain are called the principal strain axes. Their lengths define the strain magnitude and we will use the symbols X, Y, and Z to specify them, with the convention that X ≥ Y ≥ Z. In a more intuitive explanation, you may consider the strain ellipsoid as the modified shape of an initial sphere embedded in a body after the application of a homogeneous strain. We describe strain in two-dimensional space by the two axes of the strain ellipse and an angle describing the rotation of this ellipse. In three-dimensional space, therefore, we use the three axes of the strain ellipsoid and three rotation angles. This means that the strain ellipsoid is defined by six independent components, which is reminiscent of the stress ellipsoid. Indeed, the strain ellipsoid is a visual representation of a second rank tensor, but keep in mind that the stress and strain ellipsoids are not the same.

STRAIN PATH

The measure of strain that compares the initial and final configuration is called the finite strain, identified by subscript f, which is independent of the details of the steps toward the final configuration. When these intermediate strain steps are determined they are called incremental strains, identified by subscript i. The summation of all incremental strains (that is, their product), therefore, is the finite strain. We will see that there are many ways to measure finite strain in a rock, but measurement of strain increments is more difficult. Yet, incremental strain may be more crucial for unraveling the deformation history of a rock or region than finite strain. Let us explore this with a simple example (Figure 6.5).

FIGURE 6.5. The finite strains, Xf and Yf, in (a) and (b) are the same (box), but the strain path by which each was reached is different. This illustrates the importance of understanding the incremental strain history (here, Xi and Yi) of rocks and regions and inherent limitation of finite strain analysis. [4.5]

Finite strains for the distortion of a square in Figures 6.5a and 6.5b are the same, because the initial and final configurations are identical. The steps or strain increments by which these final shapes were reached, however, are very different. We say that the strain path of the two examples is different, but the finite strains are the same. The path presented in Figure 4.5a has incremental strains that reflect a strain ellipse that becomes increasingly elliptical; in other words, the ratio of the long over the short axis (X/Y) becomes greater. The path in Figure 6.5b, on the other hand, shows that the orientation of the Xi and Yi axes was perpendicular to those of the finite strain ellipse during part of the history. Consider this in a geologic context: the two paths would represent very different strain histories of a region, yet their finite strains would be identical. Obviously, an important piece of information is lost without knowledge of the strain path. It is therefore critical for structural analysis to distinguish finite strain from incremental strain. But because incremental strains are harder to determine, structural geologists imply finite strain when they loosely discuss the “strain” of a rock or a region.

COAXIAL AND NON-COAXIAL STRAIN

Earlier (Figure 6.4) we saw that strain involves the rotation of material lines. Recall that a material line is made up of a series of points in a body; for example, a row of calcium atoms in a calcite crystal or an array of grains in a quartzite. There is no mechanical contrast between the material line and the body as a whole, so that material lines behave as passive markers. All material lines in the body, except those that remain perpendicular before and after a strain increment (that is, the principal strain axes), rotate relative to each other. In the general case for strain, the principal incremental strain axes are not necessarily the same throughout the strain history. In other words, the principal incremental strain axes rotate relative to the finite strain axes, a scenario that is called non-coaxial strain accumulation. The case in which the same material lines remain the principal strain axes at each increment is called coaxial strain accumulation. These important concepts are not obvious, so we turn to a classroom experiment for further exploration.

FIGURE 6.6. Non-coaxial (a) and coaxial (b) strain. The incremental strain axes are different material lines during non-coaxial strain. In coaxial strain the incremental strain axes are parallel to the same material lines. Note that the magnitude of the strain axes changes with each step. [4.6]

First we examine the more general case of non-coaxial strain. Take a deck of playing cards (or a thick phone book) and draw a circle on the face perpendicular to the cards. By sliding the cards past one another by roughly equal amounts, the initial circle changes into an ellipse (Figure 6.6a). Draw the ellipse axes (i.e., incremental strain axes) X1 and Y1 on the face. Continuing to slide the cards produces a more elliptical shape. Again mark the ellipse axes X2 and Y2 of this second step on the cards, but use another color. Continue this action a third time so that in the end you have three steps (increments) and three X-Y pairs. Note that the last ellipse represents the finite strain. Now, as you return the cards to their starting configuration, by restoring the original circle, you will notice that the pairs of strain axes of the three increments do not coincide. For each step a different set of material lines maintained perpendicularity, and thus the incremental strain axes do not coincide with the finite strain axes. You also see that with each step the long axis of the finite strain ellipse rotated more toward the shear plane over which the cards slide. You can imagine that a very large amount of sliding will orient the long axis of the finite strain ellipse nearly parallel to (meaning, only a few degrees off) the shear plane.

In the case of coaxial strain we return to our earlier experiment with clay (Figure 6.6b). Take a slice of clay with a circle drawn on its front surface and press down on the top and bottom. When you draw the incremental strain axes at various steps, you will notice that they coincide with one another, while the ellipticity (the X/Y ratio) increases. So, with coaxial strain accumulation there is no rotation of the incremental strain axes with respect to the finite strain axes. [Note: In kinematic theory we use infinitesimally small incremental strains or instantaneous strains]

The component describing the rotation of material lines with respect to the principal strain axes is called the internal vorticity, which is a measure of the degree of non-coaxiality. If there is zero internal vorticity, the strain history is coaxial (as in Figure 6.6b), which is also called pure shear. The non-coaxial strain history in Figure 6.6a describes the case in which the distance perpendicular to the shear plane (or the thickness of our stack of cards) remains constant; this is also known as simple shear.

FIGURE 6.7. Particle paths or flow lines during progressive strain accumulation. These flow lines represent (a) pure shear, (b) general shear, (c) simple shear, and (d) rigid-body rotation. The cosine of the angle α is the kinematic vorticity number, Wk, for these strain histories is Wk = 0, 0 <Wk < 1, Wk = 1, and Wk=∞, respectively. [4.8]

Internal vorticity is quantified by the kinematic vorticity number, Wk, which relates the angular velocity and the stretching rate of material lines. Avoiding the math, a convenient graphical way to understand this parameter is shown in Figure 6.7. When tracking the movement of individual points within a deforming body relative to a reference line, we obtain a displacement field (or flow lines) that enables us to quantify the internal vorticity. The angular relationship between the asymptote and the reference line defines Wk:

Wk = cos α Eq. 6.1

For pure shear Wk = 0 (Figure 6.7a) and for simple shear Wk = 1 (Figure 6.7c). Rigid-body rotation or spin can also be described by the kinematic vorticity number (in this case, Wk = ∞; Figure 6.7d), but remember that this rotational component of deformation is distinct from the internal vorticity of strain. Using Figure 6.6 as an example, the deformation history shown in Figure 4.6a represents non-coaxial, nonrotational deformation. The orientation of the shear plane does not rotate between each step, but the incremental strain axes do rotate. The strain history in Figure 6.6b represents coaxial, nonrotational deformation, because the incremental axes remain parallel.

FIGURE 6.8. A combination of simple shear (a special case of non-coaxial strain) and pure shear (coaxial strain) is called general shear or general non-coaxial strain. Two types of general shear are transtension (a) and transpression (b), reflecting extension and shortening components. [4.7]

In natural systems, a combination of simple shear and pure shear is common, which we call general shear (or general non-coaxial strain accumulation; Figure 6.8). This is represented by the condition: 0 < Wk < 1.

SUPERIMPOSED STRAIN

The strain path describes the superimposition of a series of strain increments. For each of these increments the body is divided into regions containing material lines that extend and shorten; these regions are separated by planes containing lines with zero length change.

FIGURE 6.9. Superimposed strain. The strain ellipse contains regions in which lines are extended and regions where lines are shortened, separated by lines of zero finite elongation. (a) Coaxial superimposition of a strain event 2 produces regions in which lines continue to be extended (I), and regions where lines continue to be shortened (II), separated by regions where shortening during event 1 is followed by extension during event 2 (III). (b) Non-coaxial superimposition additionally produces a region where extension is followed by shortening during event 2 (IV). Practically this means that structures reflecting different strain states may form, especially in non-coaxial strain regimes such as shear zones. [4.9]

Considering only the two-dimensional case here (Figure 6.9) we recognize regions of extension and regions of shortening separated along two lines of zero length change in the strain ellipse. When we coaxially superimpose a second strain increment on the first ellipse, we obtain three regions (Figure 6.9a):

A region of continued extension.
A region of continued shortening.
A region of initial shortening that is now in extension.

The geometry is a little more complex when the incremental strain history is non-coaxial. Superimposing an increment non-coaxially on the first strain state results in four regions (Figure 6.9b):

A region of continued extension.
A region of continued shortening.
A region of initial shortening that is now in extension.
A region of extension that is now in shortening.

Clearly, superimposition of significant strain increments can produce complex deformation patterns in rocks. For example, extensional structures formed during one part of the deformation history may become shortened during a later part of the history, resulting in outcrop patterns that, at first glance, may seem contradictory.

STRAIN QUANTITIES

Having examined the necessary fundamentals of strain, we can now turn our attention to practical applications in structural analysis using the quantification of strain. Take the small fold with axial plane clearage shown in Figure 6.10. How much strain does this deformation feature represent? How do we go about determining this?

FIGURE 6.10. Small fold in turbidites from the Cantabrian Mountains (Spain). An axial plane cleavage is visible in the shale (gray) and sandstone (tan) layers. Hand for scale.

In the next sections we will examine strain quantification using three measures: length change or longitudinal strain, volume change or volumetric strain, and angular change or angular strain. You’ll find that all of these approaches are pertinent to the analysis of our small fold.

Longitudinal Strain

The longitudinal strain is defined as a change in length divided by the original length. Longitudinal strain is expressed by the elongation, e, which is defined as:

e = (l - lo)/lo or e = δl/lo Eq. 6.2

where l is the final length, lo is the original length, and δl is the length change (Figure 6.11a).

FIGURE 6.11. Strain quantities. The elongation, e, and stretch, s, in (a); the angular shear, ψ, and the shear strain, γ, in (b). [4.11]

Because we divide values with the same units, longitudinal strain is a dimensionless quantity. A longitudinal strain of 0.3 for a stretched rod or a continental region is independent of the original dimensions of the object. This definition of elongation implies that negative values of e reflect shortening whereas positive values of e represent extension. We label the maximum, intermediate, and minimum elongations, e1, e2, and e3, respectively, with e1 ≥ e2 ≥ e3. Remember the sign convention we just described! In practice, geologists commonly give the elongation in percent, using the absolute value, │e│× 100%, and the terms shortening and extension instead of a negative or positive sign; for example, 30% extension or 40% shortening.

Volumetric Strain

A relationship similar to that for length changes holds for three-dimensional (volume) change. For volumetric strain, Δ, the relationship is:

Δ = (V – Vo)/Vo or Δ = δV/Vo Eq. 6.3

where V is the final volume, Vo is the original volume, and δV is the volume change. Like longitudinal strain, volumetric strain is a ratio of values with the same units, so it also is a dimensionless quantity. Positive values for Δ represent volume gain, whereas negative values represent volume loss.

Angular Strain

The longitudinal and volumetric strains are relatively straightforward and easily defined strain parameters. Angular strains are slightly more difficult to handle as they measure the change in angle between two lines that were initially perpendicular. The change in angle is called the angular shear, ψ, but more commonly we use the tangent of this angle, called the shear strain, γ (Figure 6.11b):

γ = tan ψ Eq. 6.4

Like the longitudinal and volumetric strains, the shear strain is a dimensionless parameter.

Other Strain Quantities

In calculations, such as those associated with the Mohr circle for strain (see Further Exploration), we make use of a quantity called the quadratic elongation, λ, which is defined as:

λ = (l/lo)2 = (1 + e)2 Eq. 6.5

where l is the final length, lo is the original length, and e is the elongation.

The root of the quadratic elongation is called the stretch, s, which is a convenient strain parameter that directly relates to the dimensions of the strain ellipsoid:

s = λ1/2 = l/lo = 1 + e Eq. 6.6

The quadratic elongation, λ, and especially the stretch, s, are convenient measures because they describe the lengths of the principal axes (X, Y, and Z) of the strain ellipsoid:

X = s1, Y = s2, Z = s3 Eq. 6.7

with X ≥ Y ≥ Z, and

X2 = λ1, Y2 = λ2, Z2 = λ3 Eq. 6.8

FIGURE 6.12. Relationships between strain ratio (X/Y, λ1/λ2) and angular shear (ψ) for line OP that transforms into OP' with angles  and ’ and lengths lo and l before and after strain. [4.11]

Basic Strain Calculator for changes in angle and line length.

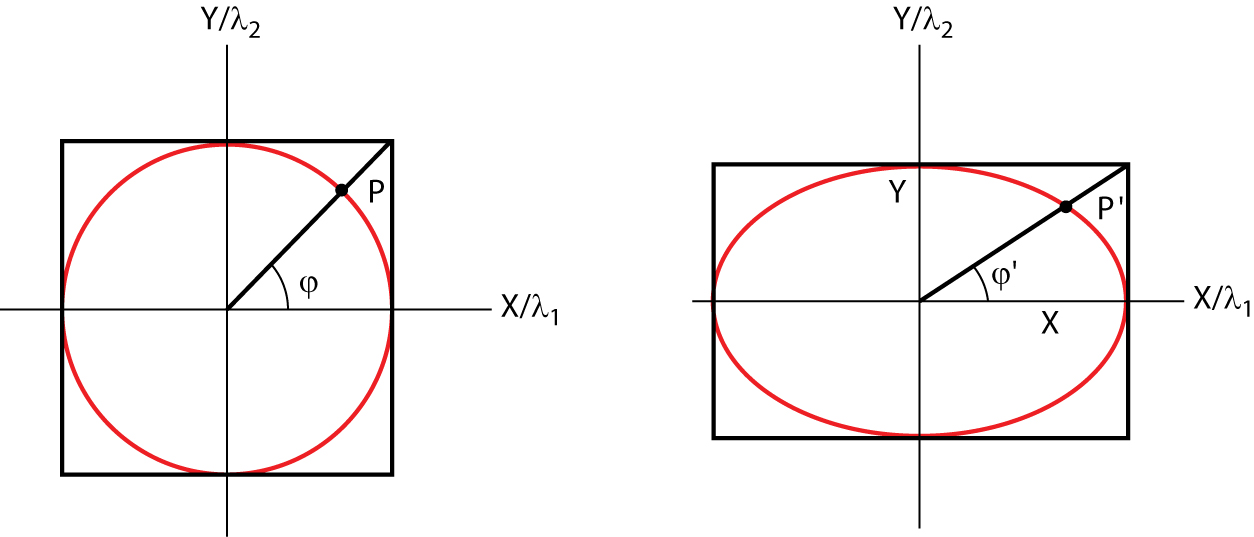
This relationship between the stretches and the strain ellipse is illustrated in two dimensions in Figure 6.12. A circle with unit radius (r = 1) becomes distorted into an ellipse that is defined by the length of axes X and Y. As a consequence of this distortion, a line OP at an initial angle of ϕ with the X-axis becomes elongated (OP') with an angle ϕ' to the X-axis. [Note: we use the symbol ' (prime) to mark the deformed state] From Figure 6.12 you can determine that the relationship between ϕ and ϕ' is described by:

tan ϕ' = Y/X ⋅ tan ϕ Eq. 6.9

or, rearranging this equation for the undeformed case:

tan ϕ = X/Y ⋅ tan ϕ' Eq. 6.10

Earlier we introduced the concept of volume change as a fourth component of deformation in which length changes occur proportionally. It is instructive to see how this affects Equations 6.9 and 6.10. In the two-dimensional case, the area of an ellipse is π(X⋅Y), thus an ellipse derived from a unit circle with area π (r = 1, so πr2 = π) implies that X⋅Y = 1. Thus, if we assume no volume change in deformed objects, and Y = 1/X, we simplify Equations 6.9 and 6.10 to:

tan ϕ' = X–2 ⋅ tan ϕ Eq. 6.11

or, for the undeformed case:

tan ϕ = X2 ⋅ tan ϕ' Eq. 6.12

Go ahead and get some hands-on experience with these relationships in the basic strain activity in Further Exploration or using the basic Strain Calculator.

You can further explore your understanding of the above manipulations by showing that Equations 6.11 and 6.12 also apply to the three-dimensional case when we assume that Y = 1, as well as that the volume is constant. The condition Y = 1 means that zero elongation occurs in the direction perpendicular to the sectional ellipse containing axes X and Z, which is a commonly made assumption in strain analysis.

Natural Strain

Earlier we distinguished between information contained in finite strain analysis from incremental strain analysis. The measure of strain that is most suitable for incremental strain histories is the natural strain. This measure of strain is no more or less “natural” than any of the other measures, but derives its name from the natural logarithm [The base of the natural logarithm (ln) is 2.72; the base 10 (log) is also used]. Natural strain does not compare the initial and final strain states, but is the summation of individual strain increments. Recall that the elongation is defined as δl/lo. This also holds for incremental strains, in which lo represents the length at the start of each strain increment. For a vanishingly small increment (or infinitesimal strain), the elongation is defined as:

ei = δl/lo Eq. 6.13

The natural strain, ε (epsilon), is the summation of these increments:

Eq. 6.14

Integrating Equation 6.14 gives:

ε = ln l/lo = ln s Eq. 6.15

Using Equation 6.6, you can also express the natural strain in terms of the elongation, e, and the quadratic elongation, λ:

ε = ln (1 + e) Eq. 6.16

ε = ½ ln λ Eq. 6.17

3D STRAIN STATES

Having defined the various strain parameters as well as their mathematical descriptions, we close by examining characteristic strain states that are based on various relationships among the principal strain axes X, Y, and Z of the strain ellipsoid. Except for simple elongation, the strain states represent constant volume conditions (that is, Δ = 0), which means that X ⋅ Y ⋅ Z = 1. These strain states are illustrated in Figure 6.13 and described below.

FIGURE 6.13. Representative Strain states. (a) General strain (X > Y > Z), (b) axially symmetric extension (X > Y = Z), (c) axially symmetric shortening (X = Y > Z), (d) plane strain (X > 1 > Z), and (e) simple shortening (1 > Z). [4.14]

General strain	State in which all three strain axes have different lengths, as defined by the relationship X > Y > Z (Figure 4.14a). This strain state does not imply anything about volume change. Also called triaxial strain.
Axially symmetric elongation	Axial strain that includes axially symmetric extension, where X > Y = Z (Figure 6.13b), and axially symmetric shortening, where X = Y > Z (Figure 6.13c). Axially symmetric extension results in a prolate strain ellipsoid, with extension occurring only in the X direction accompanied by equal amounts of shortening in the Y and Z directions (Y/Z = 1). This geometry is sometimes referred to as a cigar-shaped ellipsoid. Axially symmetric shortening requires equal amounts of extension (X/Y = 1) in the plane perpendicular to the shortening direction, Z. The strain ellipsoid assumes an oblate or hamburger shape.
Axially symmetric elongation	Axial strain that includes axially symmetric extension, where X > Y = Z (Figure 6.13b), and axially symmetric shortening, where X = Y > Z (Figure 6.13c). Axially symmetric extension results in a prolate strain ellipsoid, with extension occurring only in the X direction accompanied by equal amounts of shortening in the Y and Z directions (Y/Z = 1). This geometry is sometimes referred to as a cigar-shaped ellipsoid. Axially symmetric shortening requires equal amounts of extension (X/Y = 1) in the plane perpendicular to the shortening direction, Z. The strain ellipsoid assumes an oblate or hamburger shape.
Plane strain	State where one of the strain axes (commonly Y) is of the same length before and after strain: X > Y (= 1) > Z (Figure 6.13d). Thus plane strain is a special type of general strain, which can be conveniently described by a two-dimensional strain ellipse with axes X and Z, because no change occurs in the third dimension (Y). In many studies this particular strain state is used.
Simple elongation	State where all material points move parallel to a straight line, defined by X > Y = Z = 1 or X = Y (= 1) > Z. In these two cases, a sphere becomes a prolate ellipsoid in extension and an oblate ellipsoid in shortening (Figure 6.13e), respectively. Because two strain axes remain of equal length before and after deformation, simple elongation must involve a change in volume (Δ ≠ 0), a volume decrease in the case of simple shortening and a volume increase in the case of simple extension.

REPRESENTATION OF STRAIN

A typical goal in strain analysis is to compare results obtained in one place with those obtained elsewhere in an area or in an outcrop, or even to compare data from several different regions. When we determine strain at a locality, we assume that the volume of rock analyzed is homogeneous. Strain, however, is typically heterogeneous on the scale of a single structure, such as a fold or a shear zone, and it always is heterogeneous on the scale of mountains and orogens. Nonetheless, given a sufficiently large spatial distribution of data points we can draw important conclusions on the state of strain in a structure or a region. Whereas a listing of numerical values and orientation for X, Y, and Z, the principal strain axes, allows direct comparisons, a graphical approach to the presentation of strain data may be more informative. We’ll explore orientation and magnitude data for strain in the next sections.

Orientation

A visually appealing way to illustrate the orientation of the strain ellipsoid is to project the orientation of one or more strain axes at their respective locations in an area. This “area” may of course represent many scales, ranging from a thin section to an entire orogenic belt. You are not limited to plotting the orientation of the strain axes, but can also include information on the magnitude of strain, for example by using the strain ratio X/Z or absolute strain magnitudes as a scaling tool.

A limitation of this two-dimensional mode of representation is that we only show sections through the strain ellipsoid, something we call sectional strain ellipses. These sectional ellipses do not necessarily coincide with a plane containing one or more of the principal strain axes, the principal planes of strain, meaning that the axes of the sectional ellipse do not parallel the principal strain axes. In such cases one is left with two reasonable options: (1) draw the shape of the sectional ellipse on the surface, or (2) show the orientation of the strain axes using plunge and direction of plunge. Luckily we can often find a projection plane that is close to a principal plane of strain, so that small deviations are relatively unimportant.


FIGURE 6.14. In (a) shapes of the XY sectional ellipse of the finite strain ellipsoid are shown on a map of the Helvetic Alps in Switzerland. In (b) XZ sectional ellipses are shown in a profile constructed from this map (note that the profile plane is not perpendicular to the map surface). The map and profile show a series of NW-directed, low-angle reverse faults or thrusts in which the long axis of the strain ellipsoid lies in the direction of thrust transport and the strain ratio general increases with depth. ] 4.15]

Figure 6.14 shows an example from an area in the Swiss Alps of Europe that illustrates the informative approach of superimposing strain data on a map and on a section. We do not discuss the details of the European Alps here, but you see that the degree of strain generally increases with depth in this stack of thrust sheets (i.e., the ratio of X/Z increases with depth). The orientation of the strain ellipsoid also varies through the stack, but the long axis, X, generally points in the direction of northwesterly thrust transport and parallels the boundaries of high strain regions that separate individual thrust sheets.

Shape and Intensity

Inherently three-dimensional strain data can be conveniently represented in a two-dimensional plot, called a Flinn diagram [1], by using ratios of the principal strain axes. In fact, we’ll see later that strain analysis typically produces strain ratios rather than absolute magnitudes of the strain axes, making this type of plot particularly convenient. In the Flinn diagram for strain (Figure 6.15) we plot the ratio of the maximum stretch over the intermediate stretch on the vertical (a) axis and the ratio of the intermediate stretch over the minimum stretch on the horizontal (b) axis:

a = X/Y = (1 + e1)/(1 + e2) Eq. 6.24

b = Y/Z = (1 + e2)/(1 + e3) Eq. 6.25

The shape of the strain ellipsoid is represented by the parameter, k:

k = (a – 1)/(b – 1) Eq. 6.26

FIGURE 6.15. The Flinn diagram plots the strain ratios X/Y and Y/Z of the strain ellipsoid. Thus it offers a convenient 2D representation of a 3D geometry. The parameters k describes the shape of the strain ellipsoid. Note that volume change, denoted by Δ, is zero in this case, defining field of constriction and flattening. Δ unequal to zero represents volume gain or loss. [4.16]

The value of k describes the slope of a line that passes through the origin (angle β in Figure 4.16a). A strain sphere lies at the origin of this plot (coordinates 1,1), representing a = b = 1 or X = Y = Z = 1. Ellipsoid shapes are increasingly oblate for values of k approaching 0 and increasingly prolate for values of k approaching ∞. If k = 0, the strain is uniaxially oblate (a = X/Y = 1), and if k = ∞, the strain is uniaxially prolate (b = Y/Z = 1). The value k = 1 represents the special case for which a equals b, which is called plane strain (X ≥ Y = 1 ≥ Z). The line represented by k = 1 states separates the field of constriction (∞ > k > 1) from the field of flattening (1 > k > 0) in the Flinn diagram.

The Role of Volume Change

The foregoing descriptions assume that volume change denoted by the symbol Δ, does not occur during the strain history. To consider the effect of volume change, recall that if Δ = 0 (i.e., there is no volume change) then X ⋅ Y ⋅ Z = 1. Thus, using Δ = (V – Vo)/Vo, and substituting V = X ⋅ Y ⋅ Z and Vo = 1, we get:

Δ + 1 = X ⋅ Y ⋅ Z = (1 + e1) ⋅ (1 + e2) ⋅ (1 + e3) Eq. 6.32

which represents a straight line (y = mx + b) with unit slope (m = 1, or angle β is 45°). If Δ > 0 the line intersects the X/Y axis (volume gain), and if Δ < 0 it intersects the Y/Z axis (volume loss). In all cases, the slope of the line remains at 45°. In Figure 6.15 volume loss is illustrated. We use the terms apparent flattening field and apparent constriction field for the regions in the diagram that are separated by the line representing the plane strain conditions. The term “apparent” is used because volume change must be known to determine the actual strain state of a body. For example, the location of a strain ellipsoid in the “flattening field” may represent true flattening, but it may also represent plane strain or even true constriction conditions. These simply depend on the degree of volume loss. Like the natural strain parameter, the Ramsay plot offers a distinction between strain increments with constant ratios of volume change and those with varying ratios. In the former case the strain path is straight, whereas in the latter case the path is curved.

The parameter k describes the shape of the ellipsoid, but the position of a data point in the Flinn diagram not only describes the shape of the strain ellipsoid, but also reflects the degree (or intensity) of strain. This second element is not so readily appreciated. The farther a point in the Flinn diagram is located from the origin, the more the strain ellipsoid deviates from a sphere. But the same deviation from a sphere (i.e., the same degree of strain), occurs for different shapes of the ellipsoid, that is, for different values of k. Similarly, the same shape of the strain ellipsoid may occur for different degrees of strain. The parameter that describes the degree or intensity of strain is

i = {[(X/Y) – 1]2 + [(Y/Z) – 1]2}1/2 Eq. 6.36

So, the ability of the Flinn diagram to represent strain states and volume change and the added convenience of the Ramsay diagram to evaluate incremental strain histories present sufficient flexibility to graphically present most strain data. Listing the corresponding shape (k) and intensity (i) parameters allows for numerical comparisons among strain analyses in the same structure and/or those made over larger regions.

FINITE STRAIN MEASUREMENT

We are now ready to tackle the practical aspects of strain analysis. The determination of strain is a common task for structural geologists unravelling the geologic history of an area or examining the development of individual structures. Over the years, many methods have been proposed, some being more useful and rigorous than others. In this section, therefore, you will not find an exhaustive treatment of all methods of strain analysis; rather we limit our description to the principles, and advantages and disadvantages, of the more widely used methods. Advanced structural geology textbooks and laboratory manuals discuss related strain methods in greater detail and often present step-by-step instructions for each method. There is no doubt that the best way to learn about each method (and appreciate the assumptions) is to apply them to data sets.

The availability of personal computers and peripherals (digitizer, scanner, image analyzer) has added a new and powerful dimension to strain analysis. Increasingly sophisticated programs are available that carry out many of the more time-consuming tasks. It has become easy to obtain lots of strain data without knowing much about the methods. This “black box” approach is dangerous, because you may not realize the implicit assumptions and consider the limitations of a method. Understanding the basic tenets of strain determinations is necessary to interpret the data, so in the next few sections we focus on the fundamentals of the art of strain analysis.

Initially Spherical Objects

Recall that homogeneous strain is defined as the change in shape from a sphere to an ellipsoid. Thus, geologic features with spherical shapes are perfect for strain analysis and some of the first analyses were indeed carried out using spherical objects. The classic example involves ooids in (oolitic) limestones (Figure 6.16). Ooids are particles that have grown radially by accretion around a nucleus; commonly they are calcareous in composition. These spheres become increasingly ellipsoidal with increasing strain (Figure 6.16b and c). Some other examples of objects that are approximately spherical are vesicles and amygdules in basalt flows and reduction spots (areas where chemical change has occurred due to the presence of impurities) in shales. But keep in mind that depositional conditions may affect these strain markers; the flow of lava may stretch amygdules and compaction may affect the shape of reduction spots.

FIGURE 6.16. Ooids (a) that are deformed after (b) 25% (X/Z = 1.8) and (c) 50% (X/Z = 4.0) strain. [4.19]

Once we are convinced that our markers are initially spherical, the strain analysis of these objects is relatively straightforward. If we preserve the deformed shapes in three dimensions, we can obtain a direct representation of the shape of the strain ellipsoid by measuring the shape of the objects in three mutually perpendicular sections. In fact, these sections do not necessarily have to be perpendicular, but this simplifies the procedure. In each section we measure the long and the short axis of the sectional ellipse for several objects, which gives us ratios. The term sectional strain ellipse was used before to emphasize the fact that you do not measure the principal axes of the objects, but only their lengths in section. We combine the ratios from each of the three sections to determine the shape of the strain ellipsoid. By choosing the sections such that they coincide with the principal planes of strain (that is, the planes containing two of the principal strain axes) we simplify our procedure. In this case, we directly obtain the strain ratios (X/Y, Y/Z, and X/Z) in our three sections. Otherwise we need to use trigonometric relationships to determine the ellipsoid.

FIGURE 6.17. The long and short axes of elliptical objects are measured in three orthogonal sections. For convenience we assume that these sectional ellipses are parallel to the principal planes. The slope of regression lines through these points (which should intersect the origin) is the strain ratio in that section. In this example X/Y/Z = 2.4/1.2/1. [4.20]

An example is given in Figure 6.17. Say, you measure a ratio of X/Y = 2 in one section and in a second section, parallel to the YZ-plane of the strain ellipsoid, you measure a ratio of Y/Z = 1.2. In three dimensions this gives a ratio of X/Y/Z of 2.4/1.2/1. You can check this in a third section, containing X and Z, which should give a ratio X/Z = 2.4. Assuming that the volume remained constant (Δ = 0), you can fully specify the strain state of your sample.

X/Y/Z = 2.4/1.2/1 and Δ + 1 = X ⋅ Y ⋅ Z = 1

then

X = 2Y and Z = Y/1.2

thus

2Y ⋅ Y ⋅ (Y/1.2) = 1.7 Y3 = 1

Y = 0.8 and X/Y/Z = 1.7/0.8/0.7

Now determine what happens to the strain ratio X/Y/Z if you allow for approximately 50% volume loss (Δ = –0.5), representing a volume change that has been suggested in many studies.14 You see that, irrespective of the amount of volume change, the strain ratios remain the same, but that the magnitudes of the individual axes become smaller with volume loss (and vice versa, i.e., greater with volume gain). Consequently, the position of the strain states in Flinn diagrams remain the same with or without volume change, and thus values of k (or K) and i (or I) also remain the same. So we have no indication of volume change from our analysis of the shape of markers unless we know their original volume. To solve the critical problem of volume change we may use geochemical approaches, to which we will return in another chapter.

Variably-shaped Objects

Strained particles of all shapes have several properties in common with the finite strain ellipsoid. Material lines (meaning, arrays of particles) that are not parallel to any one of the principal strain axes will tend to rotate toward the maximum strain axis (X) and away from the minimum strain axis (Z). Material lines that are parallel to the Z-axis will undergo the greatest amount of shortening, whereas material lines that are parallel to the X-axis will have the greatest amount of extension. For an intuitive understanding of strain from non-spherical objects these two properties are most important.

FIGURE 6.18. Changes in markers of various shapes under (a) homogeneous strain, (b) coaxial, constant volume strain, and (c) noncoaxial, constant volume strain. Note the change from circle to ellipse and from an initial ellipse to an ellipse with different ratio, and the relative extension and shortening of markers. [4.21]

Figure 6.18 schematically illustrates what happens to markers with variable shapes. Although they look different, they all change in a predictable manner; but actually quantifying strain from these changes is another matter. Strain quantification is greatly simplified if the initial shape of our marker is an ellipsoid (or ellipse in the two-dimensional case of Figure 6.18), because the superimposition of ellipsoids, by definition, produces another ellipsoid. Mathematically, is it true that adding two tensors of the same rank produces a third tensor of that rank? Let’s look at this first for low-rank tensors: adding two zero-rank tensors (scalars) gives another scalar; for example, 3 + 5 = 8. Adding two first-rank tensors (vectors) produces another vector. So this indeed is a property of tensors, and therefore adding two second-rank tensors will produce another second-rank tensor. In other words, superimposing the finite strain ellipsoid on an ellipsoidal body gives an ellipsoid that contains the proper ties of both the initial ellipsoid (initial marker shape) and the superimposed ellipsoid (finite strain ellipsoid). We earlier showed this graphically when discussing superimposed strain.

FIGURE 6.19. Deformed clasts in a late Paleozoic conglomerate, US Appalachians (Narragansett, RI); camera lens for scale. [4.22]

Whereas most objects in nature are not perfect spheres, their shapes may be reasonably approximated by ellipsoids; for example, ellipsoidal clasts of a conglomerate (Figure 6.19). You will realize that we cannot simply determine the strain by measuring shapes in the deformed state of the ellipsoids, without knowing the initial shape of the objects. Two techniques are commonly used to resolve this problem: the center-to-center method and the Rf /Φ method.

Center-to-Center Method

The basic principle of the center-to-center method of strain analysis is that the distances between the centers of objects are systematically related to the orientation of the finite strain ellipsoid. 16 For example, in the XY-plane of the strain ellipsoid, grain centers that lie along the direction of the shortening axis (Y) tend to become closer during deformation than grain centers aligned with the extension axis (X). Measuring the distances of centers as a function of an arbitrary reference orientation produces maximum and minimum values that correspond to the orientation and the strain ratio of X and Y (Figure 6.20).

FIGURE 6.20. Determining strain from initially spherical or non-spherical objects using the center-to-center method. The distance between object centers is measured as a function of the angle with a reference line (a). A graphical representation of this method using 250 deformed ooids in a natural sample (b). The empty area defines an ellipse with the ratio X/Y; the angle of the long axis with the reference line is also determined. [4.23]

Computers have greatly eased the application of this principle by using a digitizer to determine grain centers and a method to graphically analyze the results. Dividing the center-to-center distance between two objects by the sum of their mean radii is a normalization procedure that better constrains the shape of the ellipsoid. Figure 6.20b shows the result of a normalized center-to-center analysis using a computer program.

Rf /φ Method

The Rf/Φ method utilizes the systematic shape changes that occur in deformed ellipsoidal objects. In a given section we measure the long and short axes of sectional ellipses and the orientation of the long axis with respect to a reference line (Figure 6.21a). For convenience we again assume that the section is parallel to the XY-plane, but this is not a prerequisite of the method.

FIGURE 6.21. Strain from initially spherical or non-spherical objects using the Rf/Φ method.

The ratios of elliptical objects are plotted as a function of their orientation relative to a reference line (a). Application of this method to 250 ooids (same sample as in Figure 4.23) shows the cloud of data points that characterizes this method. From the associated equations we determine the strain ratio and the angle of the long axis with the reference line. The values obtained from using the center-to-center and Rf/Φ methods are indistinguishable within the resolution of these methods. [4.24]

Plotting the ratio of these axes (Rf) versus the orientation (Φ) yields a cloud of data points, reflecting the addition of the initial ellipsoid (the original shape of the body) and the finite strain ellipsoid. The maximum and minimum values of Rf are related to the initial ratio (Ro) of the objects and the strain ratio (Rs; in this example X/Y), as follows:

Rf,max = Rs ⋅ Ro Eq. 6.38

Rf,min = Ro / Rs Eq. 6.39

which gives the strain ratio, Rs, by dividing Equation 6.38 by Equation 6.39:

Rs = (Rf,max/Rf,min)1/2 Eq. 6.40

The maximum initial ratio is determined by multiplying Equations 6.38 and 6.39:

Ro = (Rf,max ⋅ Rf,min)1/2 Eq. 6.41

These relationships hold when the original ratio, Ro, is greater than the strain ratio, Rs (Ro > Rs). On the other hand, if Ro < Rs, then

Rf,max = Rs ⋅ Ro (same as above), but Eq. 6.42

Rf,min = Rs /Ro Eq. 6.43

and the strain ratio and the maximum original ratio become

Rs = (Rf,max ⋅ Rf,min)1/2 Eq. 6.44

Ro = (Rf,max/Rf,min)1/2 Eq. 6.45

The orientation of the X-axis relative to the reference line in our particular example is determined by the position of Rf,max and the Y-axis is perpendicular to the X-axis in the section surface. Evaluation of the scatter of points in Rf /Φ plots is greatly eased by reference curves that are used as overlays on the data. An example of the application of this method is shown in Figure 6.21b.

Angular and Length Changes

The transformation of a sphere to an ellipsoid involves changes in line lengths as well as angular changes. Thus, methods that allow us to determine either or both of these parameters are suitable for strain determination. We will explore the principles behind some methods in the following sections.

Angular Changes

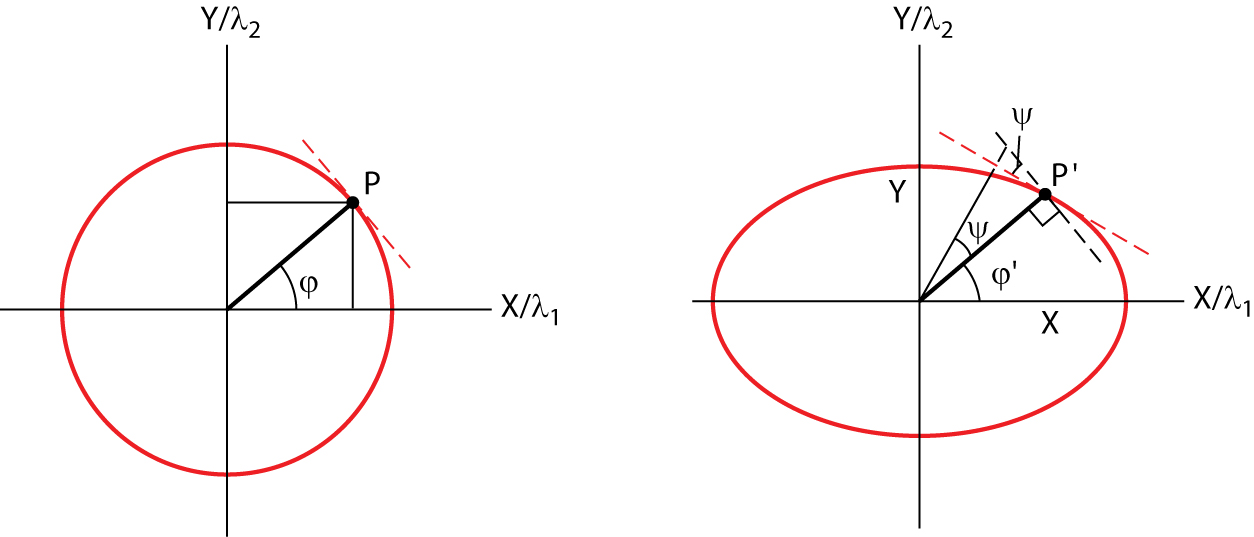
Recall the relationship between the original angle ϕ of a line, the angle after deformation (ϕ'), and the strain ratio in 2D space, X/Y:

X/Y = tan ϕ/tan ϕ' Eq. 6.46

The original angular relationships are well known in geologic objects that have natural symmetry. One suitable group of objects is fossils, such as trilobites and brachiopods, because they contain easily recognizable elements that are originally perpendicular. When we have several deformed objects available that preserve these geometric relationships, we can reliably obtain both the orientation of the strain axes and the strain ratios from their distortion.

FIGURE 6.22. Strain is determined from a collection of deformed bilaterally symmetric brachiopods (a), by constructing a graph that correlates the angular shear with the orientation (b). From this (Breddin) graph the orientation of the principal axes and the strain ratio can be determined. [4.25]

One approach is shown in Figure 6.22, which requires several deformed fossils in different orientations. Note that the method is independent of the size of the individual fossils (big ones mixed with small ones) and the presence of different species (as long as the symmetry element remains present), because only the angular changes in these objects are used in the analysis. In the plane of view, which often is the bedding plane, we measure the angular shear, ψ, for each deformed object. We plot the value of ψ versus a reference orientation (angle α), making sure that we carefully keep track of positive and negative angles. The resulting relationship is a curve that intersects the α-axis at two points (Figure 6.22b). These intersections represent conditions of zero angular shear, which coincide with the orientations of the principal strain axes in this surface, because the principal strain axes are defined as the material lines that are perpendicular before and after strain.

The strain ratio is determined using Equation 6.9 at conditions for maximum angular shear, which occurs at an angle ϕ = 45°. Substituting tan ϕ = 1 in equation 6.46, gives

Y/X = tan ϕ'max Eq. 6.47

where ϕ'max is the angle between the position of the principal axis and maximum angular shear on the α- axis (Figure 6.23b). In cases where not enough distorted fossils are available to derive a reliable curve, the strain ratio can be determined by comparison with a set of curves that are predetermined for various strain ratios. Figure 4.25 also illustrates that a population of fossils with different orientations in the plane of view allow direct determination of the orientation of the principal strain axes. By definition, fossils that do not show any angular shear must have symmetry elements that coincide with the orientation of the principal strain axes (fossils A and B in Figure 6.22).

Length Changes

Change in line lengths is possibly the easiest strain method to understand, but we postponed its discussion until now because its practical application is limited to special circumstances. A classic example of the circumstances in which longitudinal strain analysis is appropriate is shown in Figure 6.23, which illustrates two sections through a rock containing deformed belemnites.

FIGURE 6.23. Stretched belemnite from the Swiss Alps. In longitudinal view (a), calcite filling is seen between the fossil segments, whereas in sectional view (b) the marker remains circular. MN marks the sectional view. [4.26]

Recalling how strain induces a change from a circle to an ellipse, you will remember that length changes occur in a systematic manner (Figure 6.4). Given measurements of several length changes we can determine a best-fit strain ellipsoid, or ellipse in two dimensions. For this type of analysis it is most convenient to use ratios of the longitudinal strain quantities, the stretch (s = l/lo) or its square, the quadratic elongation (λ = [l/lo]), because these quantities correspond directly to the lengths of the ellipsoid axes for orientations parallel to the principal strain axes.

FIGURE 6.24. Changes in line length from broken and displaced segments of two once continuous fossils (A and B; belemnites) assuming that the extension direction (and thus ϕ') is known. Simultaneously solving equation λ' =λ1' cos2 ϕ' + λ2' sin2 ϕ' (the reciprocal of Equation 4.18) for each element gives the principal strains X and Y. An advantage of this method is that volume change (Δ) can be directly determined from the relationship X ⋅ Y = l + Δ. [4.27]

Individual stretches are readily measured if the original length of the object is known. To determine the strain ratios we need at least two different stretches and some indication of the orientation of one of the principal strain axes within that plane (Figure 6.24); without an indication of the orientation, we need at least three longitudinal strain measures. Optimally we apply this analysis in a perpendicular surface to obtain the three-dimensional strain, but this is rare in natural rocks. Strain determinations from length (and angular) changes typically give two-dimensional strain, but given appropriate assumptions (like plane strain or constant volume) the results are nevertheless quite useful. For example, the stretched belemnites in Figure 6.25 give a X/Y strain ratio of 1.23, but also indicate volume gain within this plane. Assuming constant volume strain for the rock as a whole implies that Z = 1/(X ⋅ Y) = 0.66.

LESSONS FROM STRAIN ANALYSIS

We close this chapter on deformation and strain by exploring the significance of strain analysis. After decades of work, structural geologists have produced a vast amount of finite and incremental strain data, on structures ranging from the microscale (thin sections) to the macroscale (mountain belts and continents). The aim of most of these studies is to measure strain magnitude across a region, an outcrop, or a hand specimen, in order to quantify the structural history or the development of a particular feature. For example, a sharp increase in strain magnitude in an area may define a region of high strain, like a ductile shear zone. Secondly, the meaning of strain measurements needs to be critically considered.

Patterns in Strain Quantities

Strain analysis provides general constraints on the strain required to form specific geologic structures, such as folds (Chapter 8), and foliations and lineations (Chapter 9), which can then be incorporated into the larger regional history. For example, strain determinations in samples with slaty cleavage (Chapter 9) indicate that shortening strain is greater than 50%. We can include the results of numerous other studies, but instead we will draw a few general conclusions from the large data set that is shown in Figure 6.25.

FIGURE 6.25. Compilation of finite strain values from natural markers in X/Y - Y/Z space; the corresponding X/Y and Y/Z ratios are indicated. The field inside the dashed line contains an additional 1,000 analyses, primarily from slates, that have been omitted for clarification. Plane strain conditions at constant volume (k = 1, Δ = 0) separate the fields of apparent constriction and apparent flattening, with the latter containing most strain values. Plane strain conditions accompanied by 50% volume loss are indicated by the line k = 1, Δ = –0.5. [4.30]

A compilation of hundreds of finite strain values that were obtained using a variety of techniques are plotted with the axes X/Y versus Y/Z (Figure 6.25). This large data set gives a good idea of the magnitudes of strain that are typical in natural rocks. Axial ratios range from 1 to 20 and stretches are in the range 1 < X < 3, and 0.13 < Z < 1. You also notice that most of the analyses lie in the field of apparent flattening (compare with Figure 4.16), which may be interpreted as true flattening strain or the involvement of volume loss [Note that it can also be explained by superimposition of non-coaxial strain increments, such as vertical compaction followed by horizontal shortening]. If we assume that plane strain conditions (k = 1) equally divide the number of measurements, then a volume loss on the order of 50% (Δ = –0.5) is required. One wonders, of course, where that volume of rock material went, and the role of mass transfer continues to be a topic of lively debate in the literature. The problem is further aggravated when you consider that strain values reflect the strain of the marker that was used in the determination and not necessarily that of the host rock. For many practical examples this means that the values may actually underestimate the finite strain.

Lastly, most of these data represent regional strains and exclude strains measured in shear zones. The axial ratio increases exponentially with increasing shear strain, and reported values for γ of as much as 40 in shear zones (meaning that ϕ is approaching 90°; Equation 6.3) represent extremely large axial strain ratios that lie well outside the plot—a wide range in strain magnitudes, indeed.

What Does Strain Measure?

Strain analysis attempts to quantify the magnitude and/or the orientation of the strain ellipsoid(s) in rocks and regions. In its most complete form, each strain analysis gives the lengths and orientations of the three principal strain axes. More commonly, however, we obtain strain ratios (X/Y, Y/Z, and X/Z), because we do not know the absolute dimensions of the original state. Powerful as strain quantification may appear, we need to ask two important questions.

Firstly, the strain analyzed may only represent a part of the total strain history that the rock or region has undergone. So the question is: how complete is our measurement? The second question comes about because the results of a particular strain analysis only pertain to the objects that were used for the analysis. A difference in behavior between the objects and other parts of the rock, say conglomerate clasts and their matrix, may result in a strain value for the whole rock that differs from that for the conglomerate clasts. So our second question is: how representative is our analysis? We explore this second consideration by two simple experiments that are shown in Figure 6.26.

FIGURE 6.26. In two illustrative strain experiments we deform a cube of clay with (a) a marble inclusion and (b) a fluid inclusion. If we require that the elongations in the clay are the same for both runs, the resulting elongations for the marble and fluid bubble are quite different. This illustrates the different response to stress of materials with mechanical contrast or heterogeneous systems. A practical example is strain analysis using (strong) conglomerate clasts in a (weak) clay matrix. [4.18]

We place a marble within a cube of clay, and as we load the block it deforms into a rectangular box. After sectioning, however, you learn that the marble remains undistorted! So, using the marble as the basis for strain analysis you conclude there is zero percent strain (or X/Y = 1), yet looking at the clay you clearly see that strain has accumulated. In fact, you determine a strain ratio, X/Y, of 1.8 for the clay. Now we carry out a second experiment, in which we replace the space occupied by the marble with a fluid. The result is quite different from that of the previous run. In the second case both materials show finite strain, but the strain measured from the bubble, which now has the shape of an ellipsoid, is higher than that measured from the shape of the deformed clay block. These obviously contrasting results do not represent a paradox, because all answers are correct in their own way. There is zero strain for the marble, and finite strain for the fluid bubble is greater than that for the clay block. These different results simply reflect the response of materials with different strengths. The clay is weaker than the marble, but the fluid bubble is weaker than the clay. We therefore identify strain markers of two types: passive and active markers.

Passive strain markers

Elements of the body that have no mechanical contrast; they deform in a manner indistinguishable to that of the whole body. For example, a circle drawn on our clay cube would constitute a passive marker. Such markings are rare in nature, but inclusions of the same composition as the matrix are close to this condition; for example, quartz grains in a quartzite or oolites in a carbonate. In the case of passive markers, we say that our body behaves as a homogeneous system for strain.

Active strain markers

Elelements in the body that have mechanical contrast with their matrix, and may behave quite differently. The marble and fluid inclusions in the above experiments are both examples of active markers. Conglomerate clasts in a shale matrix or garnets in a mica schists are natural examples of active strain markers, which represent a heterogeneous system for strain.

The active role of markers need not be a crippling problem as long as the strain results are considered with the limitations of each method in mind. Lastly, strain analysis can lead to misinterpretation because of an unjustified confidence in hard numbers, which has been poetically described as “garbage in, garbage out.” Always remember this simple experiment when interpreting strain data.

Back to Deformation&Strain Contents

Back to PSG&T Home

v1.4; Last update: 15-sep-23

[1] Named after UK geologist Derek Flinn