How can a strong layer of rock permanently bend into a tight fold? How can a material such as ice of a glacier distort, while remaining a solid (Figure 7.1)? Ice is a particularly instructive example of flow in crystalline solids, because it moves on human timescales. Its behavior is directly relevant to rock deformation on geologic timescales. At first one might think that solid deformation is accomplished by bending and stretching of atomic bonds in the crystal lattice, but these movements are elastic deformations and, as described in Chapter 3, elastic deformation is recoverable (i.e., nonpermanent). The movement of a glacier or the formation of a fold, however, is a permanent feature that represents ductile deformation. If we were to carefully remove a folded layer from an outcrop, or a deformed mineral from a hand specimen, they would not jump back to their original shapes. The distortions that occurred must be a result of permanent changes in the material.

FIGURE 7.1. False color images of the Malaspina Glacier (Alaska) acquired from 1986-2003 by Landsat satellites, showing moraines that are folded from differential flow of solid ice. Ice in shades of blue; moraines are brown. Scale of folding is km size. [NASA]

GMaps: https://goo.gl/maps/QiT3zVSCzVy

The principles that underlie the ability of materials, like rocks, to accumulate permanent strain are contained in a vast and ever-growing body of materials science literature. Structural geologists have increasingly applied concepts from materials science to geologic environments. The associated terminology, however, has not always remained consistent between these fields. In trying to keep new terms and concepts to a minimum, we’ve chosen to limit the coverage in this chapter; otherwise we’d lose sight of our ultimate goal: understanding the way rocks deform in Earth’s plastic regime.

VISCOSITY

Consider a beautiful waterfall. The flow of water in the river and over the ledge is an example of viscous behavior in which, with time, the water travels farther downstream. This is called viscous behavior, in which strain (displacement) accumulates as a function of time. Strain with time is defined by strain rate, which we first examine.

Strain Rate

The time interval it takes to accumulate a certain amount of strain is described by the strain rate, symbol ė, which is defined as elongation (e) per time (t):

ė = e / t = δl / (lo . t) Eq. 7.1

You recall that elongation, length change divided by original length, δl/lo, is a dimensionless quantity; thus the dimension of strain rate is [t]–1; the unit is second–1. This may appear to be a strange unit at first glance, so let’s use an example.

If 30% finite longitudinal strain (|e| = 0.3) is achieved in an experiment that lasts one hour (3600 s), the corresponding strain rate is 0.3/3600 = 8.3 × 10–5/s. Now let’s see what happens to the strain rate when we change the time duration of our experiment, while maintaining the same amount of finite strain.

Time interval for 30% strain ė

1 day (= 86.4 × 103 s) 0.35 × 10–5/s

1 year (= 3.15 × 107 s) 0.95 × 10–8/s

1 m.y. (= 3.15 × 1013 s) 0.95 × 10–14/s

Thus, the value of the strain rate changes as a function of the time period over which finite strain accumulates. Note that the percentage of strain did not differ for any of the time intervals. So what is the strain rate for a fault that moves 50 km in 1 m.y. (same as 5cm/y)? It is not possible to answer this question unless the displacement is expressed relative to another dimension of the body, that is, as a strain. We rephrase: What is the strain rate of an 800-km long fault moving 50 km in 1 m.y.? We get a strain rate of (50/800)/(3.15 × 1013) = 2 × 10–15/s. Given that most geologic structures form over millions of years, this value gives an order of magnitude for geologic strain rates.

In some cases, such as faulting, geologists may prefer to use the shear strain rate (γ˙ ). Because the differential stress is twice the maximum shear stress (see Chapter 2), the relationship between shear strain rate and (longitudinal) strain rate is:

ė = 2γ˙ Eq. 7.2

A variety of approaches are used to determine characteristic strain rates for natural processes. A widely used estimate is based on the Quaternary displacement along the San Andreas Fault of California, which gives strain rates on the order of 10–14/s. Other observations (such as isostatic uplift, orogenic processes) support similar estimates and typical geologic strain rates therefore lie in the range of 10–12/s to 10–15/s.

Now consider a small tectonic plate with a long dimension of 500 km at its divergent plate boundary. Using a geologic strain rate of 10–14/s, we obtain the yearly spreading rate by multiplying this dimension of the plate by 3.15 × 10–7/year (dimension x strain rate x duration), giving 16 cm/year, which matches the order of magnitude of present-day tectonic plate velocities. Using a human example, your 1.5-cm long fingernail grows ~1 cm per year, meaning a growth rate of 0.67/year (or 2 × 10–8/s). The rate of nail growth is therefore much, much greater than geologic rates, even though plates also “grow” on the order of centimeters. Lastly, while most geologic processes are in the range 10–12/s to 10–15/s, a few, such as meteorite impacts and explosive volcanism, are much faster (on the order of 10–2/s to 10–4/s).

Returning to the moving glacier or flowing river, we describe their time-dependent displacement as:

σ = η ⋅ ė Eq. 7.3

where σ is differential (flow) stress, ė is strain rate, and η, a constant of proportionality, called the viscosity. This

ideal type of viscous behavior is commonly referred to as Newtonian [1]7 or linear viscous behavior, but do not confuse the use of “linear” in linear viscous behavior with the linear stress–strain relationship of elasticity. The term linear is used here to emphasize its distinction from non-linear viscous (or non-Newtonian) behavior that we discuss in a later chapter.

To obtain the dimensional expression for viscosity, remember that strain rate has the dimension of [t–1] and stress has the dimension [ml–1t–2]; thus:

[η] : [ml–1t–1].

In other words, the SI unit of viscosity is the unit of stress multiplied by time, which is Pa⋅s (kg/m⋅s). In the literature we also find that the unit Poise is used, where 1 Poise = 0.1 Pa⋅s.

FIGURE 7.2. Models of linear rheologies-2. Physical model consisting of a leaky cylinder (dashpot), and associated strain–time and stress–strain rate curves for (b) viscous behavior. Symbols used: e = elongation, ė = strain rate, σ=stress, η=viscosity, t = time; vi denotes viscous component. [5.3]

The example of flowing water brings out a central characteristic of viscous behavior. Viscous flow is irreversible and produces permanent or non-recoverable strain. A physical model for this type of behavior is a leaky piston (Figure 7.2) that moves inside a fluid-filled cylinder. The resistance encountered by the moving piston reflects the viscosity of the fluid. In the classroom you can model viscous behavior by using a syringe with one end open to the air. To give you a sense of the enormous range of viscosity in nature, the viscosities of some common materials are tabulated below, ranging >25 orders of magnitude.

Material η

Air 10–5

Water 10–3

Olive oil 10–1

Honey 4

Glycerin 83

Lava 10–104

Asphalt 105

Pitch 109

Ice 1012

Glass 1014

Rock salt 1017

Sandstone slab 1018

Upper mantle 1020–1021

Lower mantle 1021–1022

Viscosities in Pa⋅s.

How does the viscosity of water, which is on the order of 10–3 Pa⋅s, compare with that of rocks? Calculations that treat the mantle as a viscous medium produce viscosities on the order of 1020–1022 Pa⋅s. Obviously the mantle is much more viscous (“stickier”) than water. You can also examine this graphically by calculating the slope of the lines for water and mantle material in a stress–strain rate diagram; the corresponding angles ϴ (Figure X.X) are 0.06° and nearly 90°, respectively. This much higher viscosity of rocks also implies that motion is transferred over much larger distances. Stir water, syrup, and jelly in a jar to get a sense of this implication of viscosity. With its viscosity of 1014 Pa⋅s, the proposed flow of glass at surface conditions has a strain rate that is much too slow to explain the sagging effect that has been mistakenly ascribed for old windows. Instead, it was simple an old manufacturing by-product and installers placing the thickest part on the bottom.

There is an enormous difference between materials that flow in our daily experiences, such as water and syrup, and the “solids” that make up the Earth. Nevertheless, we can approximate the behavior of the Earth as a viscous medium or fluid over the large amounts of time available to geologic processes (we will return to this in a later chapter). We conclude with an instructive point on stresses in Earth. Considering an average mantle viscosity of 1021 Pa⋅s and a geologic strain rate of 10–14/s, Equation 5.7 determines that differential tresses at mantle conditions are on the order of tens of megapascals, emphasizing the distinction between large lithostatic (=load) stress and small differential (=flow) stress at depth that we discussed earlier.

In this chapter we turn our attention to the mechanisms and processes of deformation in the Earth’s Plastic Regime. To refresh your memory—strain that is distributed over the body rather than localized is what distinguishes ductile behavior from brittle behavior. But strain that appears homogeneous on one scale may represent heterogeneity on another, so again we need to include the scale of our observation. As scales of observation in structural geology range from nanometers (10–9 m) to kilometers, single minerals to mountain ranges, we define ductile behavior as uniform flow down to the scale of the hand specimen, that is, down to the mesoscopic scale.

Earlier we saw that ductile behavior can occur in the Frictional Regime by the process of cataclasis. We recognize two mechanisms for deformation in the Plastic Regime:

Dislocation creep;
diffusional mass transfer.

Which processes dominate at a given time in a rock’s history is primarily a function of temperature, stress, strain rate, grain size, composition, and fluid content. Temperature, in particular, is an important parameter, but minerals behave differently at different temperatures. What is considered high-temperature behavior for one mineral is low-temperature behavior for another mineral. Thus, when talking about the relationship between temperature and deformation, we introduce a normalized parameter that is called the homologous temperature, Th. The homologous temperature is a dimensionless parameter that is defined as the absolute temperature divided by the melting temperature (in K) of the material:

Th = T/Tm Eq. 7.4

where T is temperature and Tm is melting temperature of the material, both in K (kelvins). In this chapter we define three temperature domains in Earth:

Low-temperature domain 0 < Th < 0.3

Medium-temperature domain 0.3 < Th < 0.7

High-temperature domain 0.7 < Th < 1

After discussing the fundamental mechanisms and their associated microstructures (i.e., mineral geometries on the microscopic scale), we close this chapter by examining the interrelationship between the various rheologic parameters, and by introducing the powerful concept of deformation mechanism maps.

CRYSTAL DEFECTS

Deformation of materials at elevated temperatures in Earth is promoted by the motion of crystal defects. In simple terms, a crystal defect is an error in the crystal lattice, and there are three basic types:

(1) point defects,

(2) line defects or dislocations,

(3) planar defects or stacking faults.

The motion of defects gives rise to permanent strain without the material losing cohesion (i.e., without fracturing). Point and line defects are most important for the deformation of rocks. Planar defects, which arise from errors in the internal layering of minerals, play only a limited role in deformation. In order to understand diffusional mass transfer and crystal plasticity, we first need to take a more detailed look at point and line defects.

Point Defects

FIGURE 7.3. Point defects: (a) vacancy, (b) substitutional impurity (blue), (c) interstitial impurity (red), (d) vacancy migration. [9.4]

We identify two types of point defects, vacancies and impurities. Vacancies are unoccupied sites in the crystal lattice (Figure 7.3a). Impurity atoms are substitutionals, in which an atom in a lattice site of the crystal is replaced by a different atom (Figure 7.3b) or interstitials, in which an atom is at a non-lattice site of the crystal (Figure 7.3c). Vacancies can migrate by exchange with atoms in neighboring sites (Figures 7.3d). At first glance, the concept of migrating vacancies sounds a bit odd, but when an atom moves into a vacant site, you can equally say that the vacancy moved. The general term for this process of atom or vacancy migration is diffusion. This important process is discussed later in the chapter. When we apply a differential stress to a crystal, this causes a gradient in the vacancy concentration. Vacancies migrate down these concentration gradients, which causes solid material to flow.

Line Defects (or Dislocations)

A line defect, usually called a dislocation, is a linear array of lattice imperfections. More formally, a dislocation is the linear array of atoms that bounds an area in the crystal that has slipped relative to the rest of the crystal (Figure 7.4). This definition is hardly informative at this point, so we first look at the geometry of two end-member configurations, the edge dislocation and the screw dislocation, before turning to the concept of slip in crystals.

FIGURE 7.4. Geometry of a dislocation. (a) The edge and screw-type dislocations and their geometrical relationship. The boundary between the unslipped and slipped portion of the crystal is the dislocation line, l (red line); (b) the extra half-plane of atoms in an edge dislocation; (c) the corkscrew-like displacement of the screw dislocation. [9.6/9.7]

An edge dislocation occurs where there is an extra half-plane of atoms in the crystal lattice. As illustrated in Figure 7.4a, there are 7 vertical planes of atoms at the top half of the crystal and only 6 vertical planes of atoms at the bottom half. The termination of the extra half-plane (the plane that ends halfway in the crystal) is the dislocation. It extends into the crystal as the dislocation line, l (line CD in Figure 7.4a). The symbol for an edge dislocation is ⊥ or ⊤ depending on whether the location of the extra half-plane is above or below the associated glide plane of the crystal (see further). Imagine an axe that is stuck in a piece of wood. The presence of a dislocation causes a distortion of the crystal structure, just like a wedge distorts the log that is being split.

In a screw dislocation, the atoms are arranged in a corkscrew-like fashion (Figure 7.4); the axis of the screw marks the dislocation line (line CD in Figure 7.4c). A useful analogy of the geometry of a screw dislocation is a car parking garage, in which ramps carry cars up or down to individual floors. Many geologists, however, much prefer the corkscrew analogy.

FIGURE 7.5. Determination of the Burgers vector, b (red arrow), of a dislocation using a Burgers circuit. (a) The Burgers circuit around an edge dislocation (marked by l, blue). (b) The Burgers circuit in a screw dislocation. The closure mismatch for both edge and screw dislocations is the Burgers vector, b. In the edge dislocation b is perpendicular to l, and in the screw dislocation b is parallel to l. [9.8]

In a deformed crystal, an atom-by-atom circuit around the dislocation fails to close by one or more atomic distances, while a similar circuit around atoms in a perfect crystal would be complete. The arrow connecting the two ends of the incomplete circuit is called the Burgers vector, b. The length of the Burgers vector in most minerals is on the order of nanometers (1 nm = 1 × 10–9 m). For an edge dislocation, the Burgers circuit remains in the same plane (Figure 7.5a), while for a screw dislocation the circuit steps up or down to another plane (Figure 7.5b).

Edge and screw dislocations can, therefore, be distinguished on the basis of the relationship between the Burgers vector and the dislocation line. For edge dislocations, the Burgers vector is perpendicular to the dislocation line, (Figure 7.5a) and for screw dislocations, the Burgers vector is parallel to the dislocation line (Figure 7.5b). These properties are used to determine the nature of imaged dislocations revealed by the electron microscope. Edge and screw dislocations are only end-member geometries; dislocations that consist of part edge and part screw components are called mixed dislocations. Besides being visible at very large magnifications in the electron microscope, crystal defect features may be indirectly seen by using a decoration technique (see appendix at the end of this chapter). Figure 7.6 shows an optical image of dislocations in the mineral olivine using a special decoration technique that marks their location.

FIGURE 7.6. Dislocations in olivine from a Hawaiian mantle nodule. The dislocations appear by a decoration technique (described in Supplementary Material), which allows for their recognition in the optical microscope. Width of view is ∼200 μm. [9.9]

Earlier we mentioned that the presence of dislocations distorts the crystal lattice, which gives rise to a local stress field around a dislocation. In an edge dislocation (Figure 7.7a) there is compressive stress on the side of the extra half-plane of atoms and tension on the opposite side. The earlier wood-splitting analogy serves to illustrate this pattern. The axe forces the wood apart, giving rise to compression, which may result in the axe becoming stuck. Just beyond the tip of the blade, however, there is tension, which is why you can split wood without the blade going all the way through. Similarly, in a screw dislocation we introduce shear stresses (Figure 7.7b).

FIGURE 7.7. Geometry of the stress field (shaded region) around an edge dislocation (a) and around a screw dislocation (b). [9.10]

What is the effect of these local stresses? The role of compressive and tensile stresses is analogous to the behavior of magnets and charged particles. The compressive stress fields of edge dislocations repel, while the compressive and tensile fields of edge dislocations attract (Figure 7.8), just like the poles of two magnets attract or repel when their polarities are reversed.

FIGURE 7.8. Interactions between neighboring edge dislocations. Regions labeled C and T are areas of compression and tension, respectively, associated with each dislocation.

(a) Like dislocations on the same or nearby glide planes repel. (b) Like dislocations on widely separated glide planes may attract or repel depending on the angle between the lines joining the dislocations. (c) Unlike dislocations on the same or nearby glide planes attract. [9.11]

Similarly, screw dislocations with the same sense of shear repel each other and those with opposite senses of shear attract. In a crude way you can say that dislocations are able to “see” each other by the stress fields they generate from the distortion of the crystal lattice. Later we will see that these distortions provide the energy for dislocations to move, producing permanent shape change (=strain) of the crystal, toward lowering the internal strain energy. Note that stress from internal distortions is not the same as the stress arising from, for example, squeezing a crystal.

Edge and screw dislocations are end-member configurations, called perfect dislocations, because the Burgers vector has a length of one unit lattice distance (i.e., the length of one atomic bond, or multiples thereof). However, studies of minerals (e.g., calcite) have shown Burgers vectors that differ from one unit lattice distance; these are called partial dislocations. Partial dislocations may be formed by splitting a long Burgers vector into two or more components by the process of dissociation. Dissociation is energetically more favorable because it involves smaller displacements. Such arrays of partial dislocations produce, for example, twinning in calcite crystals.

CRYSTAL PLASTICITY

Dislocations are able to migrate through the crystal lattice if the activation energy for movement is achieved. The distortion of the crystal lattice around dislocations is one source of driving energy, as the system tries to achieve a lower internal strain energy. Applying a differential stress is another driving mechanism for dislocation motion. The associated distortion of solid phases is called crystal plasticity. Dislocation movement may occur by glide or a combination of glide and climb (creep), depending mainly on temperature. A third case of crystal-plastic behavior, mechanical twinning, occurs at low temperatures in some minerals. Before we describe the various mechanisms, we generalize their temperature domains and microstructural processes as follows:

Low-temperature plasticity 0 < Th <.3

dislocation glide
- mechanical twinning
- twinning

Medium-temperature plasticity .3 < Th <.7

dislocation glide
dislocation climb
- recovery
- recrystallization

High-temperature plasticity .7 < Th <1

grain boundary sliding superplasticity (GBSS)

Th is homologous temperature: T/Tmelting (in K).

For example, quartz: Tmelting is ~1975 K (~1700oC)

Qz plasticity at (1975 x 0.3) ≈ 590K (≈ 315oC)

DISLOCATION CREEP

Dislocation Glide

Deformation and temperature introduce energy into the crystal, which allows dislocations to move. However, dislocations are not free to move in any direction through the crystal. At low temperatures glide is restricted to glide planes (or crystal slip planes). The glide plane of a dislocation is the crystal plane that contains the Burgers vector, b, and the dislocation line, l. Because a plane is defined by two nonparallel lines, each edge dislocation has one slip plane, because b and l are perpendicular. A screw dislocation on the other hand has many potential slip planes, because b and l are parallel. In crystallographic terms, a glide plane is a crystallographic plane across which bonds are relatively weak. Some crystals have only one crystallographic plane that is an easy glide plane; others may have many. In the Supplementary Material section we lists the dominant slip systems for some of the more common rock-forming minerals. Note that in many crystals more than one slip system may be active under similar conditions.


FIGURE 7.9. Dislocation glide. (a) Movement of an edge dislocation, which may be likened to the movement of a caterpillar. (b) Movement of a screw dislocation, which is analogous to tearing a sheet of paper, with the screw dislocation at the tip of the tear. After the dislocation passes through the lattice, it leaves behind a strained crystal with a perfect crystal lattice structure. The dislocation line, l (red), glide direction (arrow) and glide planes (red) are shown. [9.12] Animation.

What is the actual process that allows the movement of dislocations? Nature has devised an energetically clever way for dislocations to move. Rather than simultaneously breaking all atomic bonds across a plane, such as occurs during fracturing, only bonds along the dislocation line are broken during an increment of movement. This requires much less energy than fracturing. Let us again turn to an analogy to illustrate this. The movement of dislocations is comparable to moving a large carpet across a room that contains heavy pieces of furniture. The easiest way to move the rug is to ruck up one end and propagate the ruck across the room. Energy is only needed to lift up selected furniture legs to propagate the ruck past these obstacles rather than lift all the furniture simultaneously. In nature, caterpillars and snakes move similarly by displacing one segment of their body at a time (Figure 7.9), instead of moving their entire body simultaneously.

An edge dislocation moves by successive breaking of bonds under the influence of a minimum stress acting on the glide plane, which is called the critical resolved shear stress (CRSS). If a crystal has several potential glide planes, it is likely that, for a given applied stress, the CRSS is exceeded on at least one and sometimes more than one of these glide planes. An edge dislocation moves when the unattached atoms at the bottom of the extra half-plane bond to the next atoms that are located directly below the glide plane. Thus the position of the extra half-plane moves relative to the dislocation without breaking all bonds in the extra half-plane (Figure 7.9a).

A screw dislocation moves forward by shearing one atomic distance (Figure 7.9b), similar to tearing a piece of paper. While atomic bonds are broken and reattached when dislocations move toward the edge of a crystal, they leave a perfect crystal lattice behind. When a dislocation reaches the edge of the grain there are no more atoms below to attach to and the crystal becomes offset. This offset of the crystal edge produces stair-step structures on the surface of the crystal known as slip bands, which are sometimes visible on large crystal surfaces. Thus, the process of dislocation movement produces permanent strain without the material ever losing coherency.

Cross-Slip and Climb

It is not always possible for dislocations to propagate to the edge of the crystal. Point defects, such as impurity atoms that are bonded tightly to their neighbors, can resist the breaking of bonds that is required for dis location glide. Unfavorable stress fields of the dislocations themselves can also resist their motion, especially when many dislocations are present. Just consider trying to work your way past a car accident slowing the traffic in your lane, or even bringing it to a complete halt. Not surprisingly, obstacles that result from the presence of many immobile dislocations are called pile-ups. In order to overcome these obstacles, edge and screw dislocations must move out of their current glide plane, which they do by the processes of climb and cross-slip, respectively. The processes require additional energy beyond that for dislocation glide.

FIGURE 7.10. Cross-slip of a screw dislocation, facilitated by diffusion of atoms (arrows). [9.13]

Screw dislocations, unlike edge dislocations, are not confined to a single glide plane, because the dislocation line and Burgers vector are parallel. They can therefore leave one glide plane and move to another glide plane with relative ease, a process called cross-slip (Figure 7.10). If it is so easy, why does cross-slip not occur all the time? Cross-slip requires that the dislocation abandons a favored glide plane (one with a short Burgers vector) for a less-favored one, and thus cross-slip takes place only if the CRSS on the less favored plane is increased. Alternatively, raising the temperature lowers the CRSS that is needed for cross slip, because atomic bonds are weakened, and cross-slip occurs more easily.

FIGURE 7.11. Climb of an edge dislocation is facilitated by diffusion of atoms (arrows). [9.13]

Edge dislocations cannot cross-slip because they have only one glide plane. However, they can climb to a different, parallel glide plane if there are vacancies to accept the lowest atoms of the extra half-plane (this is shown two-dimensionally in Figure 7.11). Climb, therefore, involves diffusion (see further), and because the rate of vacancy production increases with rising temperature, the efficiency of dislocation climb is temperature dependent.

Both cross-slip and climb are activated at temperature conditions that exceed those for dislocation glide in a mineral given the same stress conditions, and therefore they typically occur at deeper (i.e., hotter!) levels in the Earth. Although it is not possible to identify a fixed depth at which cross-slip and climb occur, because this is a function of the mineral as well as Earth’s thermal structure, as a general guide, we can specify the temperature values at which these processes occur for different minerals. Glide and climb occur at temperatures greater than 300°C for quartzitic rocks and carbonates, and at higher temperatures (>500°C) for such common minerals as dolomite, feldspar, and olivine. In the literature you find that the term dislocation creep is used for the combined activity of glide and climb.

FIGURE 7.12. (a) Two edge dislocations with opposing extra half-planes that share a glide plane move in opposite directions to meet and form a perfect crystal. (b) When they move in different glide planes, a vacancy is formed when they meet, which nonetheless represents a lower distortional state. [9.14]

While like dislocations often repel one another, unlike dislocations attract and may annihilate each other, as we saw earlier. Dislocation annihilation is one way of reducing the internal strain energy that arises from lattice distortions in a crystal. For example, two edge dislocations lying in the same glide plane with the extra half-plane of one dislocation inserted upwards (positive edge dislocation) and the other downward (negative edge dislocation) annihilate each other (Figure 7.12a). Similarly, convergence of screw dislocations with Burgers vectors in opposite directions also results in annihilation. Two dislocations of opposite sign but on different glide planes may still attract, but they cannot fully annihilate each other. In such cases, a point defect remains (such as a vacancy; Figure 7.12b). Because climb and cross-slip increase the probability of dislocation annihilation, the rate of dislocation annihilation is also temperature dependent.

Strain and Dislocations

We learned previously that dislocations are not stationary elements of a crystal, but are able to move (glide), and that they leave behind what is called the slipped portion of the crystal. Perhaps surprisingly, this slipped portion has no crystallographic distortion after the dislocation has passed through this part of the crystal. This ability of dislocation to move through a crystal brings us back to the earlier definition of a dislocation that was given without much explanation at the time: a dislocation is the linear array of atoms that bounds an area in the crystal that has slipped one Burgers vector more than the rest of the crystal. Having examined the various dislocation motion mechanisms, we need to recognize an important distinction between dislocation glide on the one hand, and dislocation cross-slip and climb on the other hand.

Dislocation glide is the process that produces a change in the shape of grains; it is therefore the main strain-producing mechanism of crystal plasticity. Cross-slip and climb facilitate dislocation glide, but by themselves produce little finite strain; they allow a dislocation to leave its original glide plane, to bypass an impurity, for example. Cross-slip and climb are therefore the rate-controlling mechanisms of crystal plasticity, and limit the resulting strain rate. Because climb occurs at temperatures that are higher than those required for glide in a mineral, you also find the terms low-temperature creep for dislocation glide (and twinning) and high-temperature creep for dislocation glide plus climb.

WHERE DO DISLOCATIONS COME FROM?

Nothing in life is perfect! You have undoubtedly heard and probably experienced this yourself, and the same goes for a mineral’s life. Defects, such as dislocations, are a part of all minerals, for good reasons: The small offsets that occur at the edges of crystals containing dislocations (on the order of nanometers) are used as nucleation sites during mineral growth; while for deformation, dislocations are necessary to enable the shape change during crystal plasticity. So far, we have only talked about the situation where a couple of dislocations occur at the same time, but the number of dislocations in a mineral, the dislocation density, N, is actually quite large. For example, “perfect” grains that have grown from a melt have a dislocation density of 106 cm–2, and this density is several orders of magnitude larger in deformed grains. Even near perfect crystals that are grown in the laboratory still have thousands of dislocations per square centimeter (cm2). So what is this strange unit “cm–2” for dislocation density? Dislocation density, N, describes the total length of dislocations per volume of crystal; thus

N : [l] / [l3] = [l–2].

Measuring dislocation length per unit volume is not a very convenient way to determine N, so practically we measure the number of dislocations (dimensionless scalar) that intersect an area (l2), which gives the unit [l–2]. Later we will give an example of a dislocation density calculation.

FIGURE 7.13. Dislocation multiplication in a Frank-Read source. (a) A pinned dislocation with Burgers vector, b, bows out during glide (b–g) to form a new dislocation (h). The slipped portion of the grain is shaded. [9.19]

In order to obtain appreciable strains from dislocation movement, we will need a great many dislocations. We have already learned that strain is produced by dislocations moving to the edge of the crystal, leaving a perfect lattice behind. So, in order for crystal plastic processes to proceed we actually need to generate dislocations. We earlier mentioned that dislocation density is greater in strained grains than in unstrained, “perfect” grains, which suggests that dislocations are generated during deformation. One mechanism for dislocation generation (or multiplication) is by Frank-Read sources (Figure 7.13). Consider a dislocation that is anchored at two points, A and B; this pinning may arise from impurities, climb, or interaction with other dislocations (not shown in the figure). During glide, the A–B dislocation will bow out because it is pinned at its edges (Figure 7.13b-d), and eventually this produces the kidney-shaped loop in Figure 9.19e and 9.19f. Note that the dislocation segments at A and B in Figure 7.13 are opposite in sign because their Burgers vectors are opposite. So as A and B come together they annihilate (Figure 7.13g), forming a new A–B dislocation line, while leaving the old loop present (Figure 7.13h). The process starts again for the new A–B dislocation line while the first loop continues to glide. Because there is no restriction on the number of cycles, a great many dislocation loops are generated in this manner, which occurs for both edge and screw dislocations. This and other dislocation multiplication mechanisms collectively produce the high dislocation densities that are required for grains to deform by crystal plastic processes.

DEFORMATION MICROSTRUCTURES

Can we recognize the (past) activity of a particular deformation mechanism and, by inference, determine the rheologic conditions during deformation? The answer to this question is mostly yes, because deformation mechanisms produce relatively characteristic microstructures that can be observed in hand specimens and thin section. However, a rock’s “memory” can be incomplete; only the latest deformation mechanism may be preserved. Once we establish the operative deformation mechanism from microstructures we can proceed to make predictions about the conditions of temperature, stress, and strain rate during deformation, which is the ultimate reason to study microstructures. Throughout the text we use the term microstructure to describe geometric characteristics of rocks on the scale of the microscope; for example, twins are a microstructural element. We use the term (micro)fabric, as it means different things to different people, with an appropriate modifier, such as dimensional-preferred fabric for geometric alignments or crystallographic-preferred fabric, that describes the degree of crystal lattice orientation of a mineral aggregate.

In the next several pages we look at the characteristic microstructures in deformed rocks that arise from four mechanisms: mechanical twinning, recovery, recrystallization, and superplastic creep. To assist you with the many new concepts that will be introduced, brief descriptions of the processes, characteristic microstructures, and some related terms of crystal plastic and diffusional creep are given in the Supplementary Material section.

Mechanical Twinning (Low-T Plasticity)

Twins are a common feature in many minerals. You may see them with the hand lens in the minerals plagioclase and calcite. In thin section, under crossed polarizers, they are easily recognized by their extinction behavior and lathlike shape as you rotate the stage. Twins that develop during the growth of a crystal, called growth twins, say little or nothing about the conditions of deformation (i.e., stress and strain). In contrast, minerals such as calcite form twins in response to an applied stress; these are called mechanical twins (Figure 7.14).

FIGURE 7.14. Calcite e-twins in experimentally-deformed marble. Width of view is ∼4 mm. (Courtesy S Schmid) [9.15]

We’ll first have a look at twinning in general and then see what information mechanical twins can provide for deformation studies. Mechanical twinning is a type of crystal plastic process that involves the glide of partial dislocations. A surface imperfection, the twin boundary, separates two regions of a twinned crystal. The lattices in these two portions are mirror images of each other; in other words, a twin boundary is a mirror plane with a specific crystallographic orientation. As a rule, twinning planes cannot already be mirror planes in the non-twinned crystal, and mechanical twinning is therefore most common in low-symmetry minerals such as trigonal calcite and dolomite, and triclinic feldspar. Recall that crystal symmetry is a geometric operation that repeats a crystal plane in another position.

FIGURE 7.15. Mechanical twinning and dislocation glide (a). The heavy outline marks a twinned grain, in which twin boundaries (heavy dashes) are mirror planes. The atomic displacements are of unequal length and typically do not coincide with one atomic distance (partial dislocation). Closed circles are atoms in final structure and open circles give the original positions of displaced atoms. Twinning is a special type of dislocation glide (b). In the latter, atoms move one or more atomic distances in the glide plane (heavy dashed line). [9.16]

Mechanical twins are produced when the resolved shear stress acting on the future twin boundary exceeds a critical value (the CRSS for twinning). During twinning, the crystal lattice rotates in the direction that produces the shortest movement (smallest linear displacement) of atoms, with a unique rotation angle. As such, mechanical twinning has similarities with dislocation glide, but differs in two aspects. First, atoms are not moved an integral atomic distance as in glide, but rather only by some fraction of the atomic distance; consequently, twinning involves partial dislocations. Secondly, the twinned portion of a grain is a mirror image of the original lattice (Figure 7.15a), whereas the slipped portion of a grain has the same crystallographic orientation as the non-slipped portion of the grain (Figure 7.15b). In deformation studies we are interested mostly in mechanical twinning; that is, twins produced by stress, which are recorders of strain and the regional stress pattern. In Further Exploration we describe calcite twinning analysis, which is very useful in studying stress and strain fields in limestones/marbles subjected to small strains, the kinematics of folding, the formation of veins, the early deformation history of fold-and-thrust belts, and deformation patterns in continental interiors.

Recovery (Low- to Medium T Plasticity)

The presence of crystal defects such as dislocations and twins increases the internal strain energy of a grain, because the crystal lattice surrounding the defects is distorted. The atomic bonds are bent and stretched (to give the “strain” in strain energy), so that the crystal lattice is not in its lowest energy state. Dislocation creep lowers the internal strain energy by annihilation and/or moving dislocations to the edge of crystals, so that the internal strain is minimized. This is the reason that internal strain energy is also called the stored strain energy. However, this does not mean that internal strain is recoverable (as in elastic strain), because permanent distortions are produced around dislocations in the crystal. Another way to change the internal strain energy of a grain is by reorganization and localization of crystal defects.

FIGURE 7.16. Irregularly distributed dislocations (a) are rearranged by glide and climb to form a dislocation wall (or tilt boundary) that separates subgrains (b). [9.24]

As a result of climb, cross-slip, and glide, dislocations can be arranged into a zone of dislocations, called a dislocation wall or tilt boundary. Such tilt boundaries produce a lower strain energy state in most of the grain than when dislocations are more evenly distributed across the grain (Figure 7.16). A single dislocation produces only a small crystallographic distortion that is not visible optically, but an array of dislocations in a tilt boundary makes the crystallographic mismatch optically visible. The greater the number of dislocations in the wall, that is, the closer their spacing, the greater the crystallographic mismatch across the boundary.

FIGURE 7.17. A tilt boundary composed of edge dislocations at a distance h apart in a simple lattice. The crystal lattice across the boundary does not have the same orientation, but is rotated over an angle θ; b is the Burgers vector and h is the spacing of dislocations in the tilt wall. [9.25]

The angular mismatch, θ, across a tilt boundary is a function of the length of the Burgers vector (b) of a dislocation and the spacing (h) of individual dislocations in the wall (Figure 7.17):

2 sin(θ/2) = b / h Eq. 7.5

We call the region of a large crystal that is enclosed by a low-angle tilt boundary a subgrain. The convention to distinguish between low-angle (subgrains) and high-angle boundaries (recrystallized grains; discussed later) is an angular difference across the tilt boundary that is less than 10°. With this information we can estimate the number of dislocations in a tilt wall 0.5mm long by 4nm wide (using Equation 7.5), assuming a Burgers vector of 0.5 nm length and an angular mismatch θ of 10°. This implies that the dislocation spacing, h, is approximately 3 nm and thus that there are more than ~165,000 dislocations in this 0.5mm long low-angle tilt boundary, representing a dislocation density in the area of the low-angle tilt wall (2 × 10–6mm2) of 3.3 × 1011mm–2. This is many orders of magnitude greater than dislocation density in undeformed crystals.

FIGURE 7.18. Subgrain microstructure and wavy (or undulose) extinction in a quartzite.

View is ~4x5 mm. [9.26]

In thin section, especially under cross-polarized light, undulatory extinction is one manifestation of the crystallographic mismatch that produces subgrains. It is particularly common in the minerals calcite, quartz, olivine, and pyroxene (Figure 7.18). Recovery is the name of the process forming low-angle or subgrain boundaries by the temperature-activated rearrangement of dislocation, which produces the characteristic subgrain deformation microstructure. In the case of phyllosilicates, such as muscovite, these subgrains are also called a polygonized microstructure, which describes the arch-like geometry where each segment is oriented at a slightly different angle from the next. Experiments in which recovery dominates have shown that the stress function of the associated flow law is exponential, as we will explore later; we, therefore, also see the term exponential-law creep for recovery microstructures.

Recrystallization (Medium-T Plasticity)

The process removing the internal strain energy that remains in grains after recovery is called recrystallization; it forms high-angle grain boundaries that separate relatively strain-free grains from each other (optical angle minimally 10o, but usually much more). In rocks, a recrystallized microstructure is characterized by grains without undulatory extinction and with relatively straight grain boundaries that meet at angles of about 120° (Figure 7.19).

FIGURE 7.19. Recrystallization microstructure in a synthetic material (OCP), showing relatively strain-free grains with straight grain boundaries. Width of view is ∼2 mm. (Courtesy W. Means) [9.27]

A real-time example of this process can be seen in the foam of soap. Looking closely at foam while washing the dishes or your hair, you will see all the geometric characteristics of a recrystallized microstructure. Because some of the same energy considerations are involved in the structure of foam, we also call the microstructure of recrystallized rock a foam structure.

Recrystallization within an anisotropic stress field (i.e., a differential stress) is called dynamic recrystallization. It results in grainsize reduction, which is well known from sheared rocks, such as mylonites. We return in more detail to mylonites elsewhere, but here we note that they have a grain size that is smaller than that of the host rock from which they formed. In fact, the term mylonite is unfortunate for these microstructures as it derives from the Greek word “mylos,” meaning milling. At the time of their discovery in northern Scotland [2] it was thought that they were formed by a grinding process (which we now call cataclasis). Since their original discovery we have learned that this is incorrect, and that dynamic recrystallization is responsible for grain-size reduction; nonetheless, the name mylonite has persisted. Based on experimental work, dynamic recrystallization can be used as a semi-quantitative indicator of the temperature conditions during deformation; for example, recrystallization begins at ∼300°C for calcite, ∼350°C for quartz, and ∼450°C for feldspar. These estimates seem to agree well with temperature estimates in deformed natural rocks.

Recrystallization occurring under isotropic stress conditions or when the differential stress is removed is called static recrystallization; otherwise known as annealing in the materials science community. From a microstructural perspective the only thing that distinguishes static recrystallization from dynamic recrystallization is a relatively larger recrystallized grain size. Static recrystallization reduces the internal strain energy by the formation of relatively large, strain-free grains that grow to decrease the total free energy of the rock. Figure 7.20 uses a synthetic material to illustrate the difference between microstructures from dynamic and static recrystallization.


(a) Dynamic recrystallization: Relatively small grain size Straight grain boundaries Relatively fine “foam” texture Strain (or work) softening Link	(b) Static recrystallization (annealing): Relatively large grain size Straight grain boundaries Relatively coarse “foam” texture Link (OCP experiments courtesy W. Means)
FIGURE 7.20. Differences between (a0 dynamic recrystallization and (b) static recrystallization, with animations.

We close with a comment about the use of the term recrystallization. Recrystallization as used in structural geology involves changes in the strain energy of a single phase, whereas the term recrystallization in petrology involves multiple phases. In petrology, the process is governed by chemical potentials rather than by strain potentials that drive dislocation movement. Both are correct, but be sure not to confuse these very different uses of the term recrystallization.

Mechanisms of Recrystallization

There are three main mechanisms by which recrystallization proceeds, rotation recrystallization, subgrain coalescence and migration recrystallization. Rotation recrystallization describes the progressive misorientation of a subgrain as more dislocations move into the tilt boundary, thereby increasing the crystallographic mismatch across this boundary. This produces a high-angle grain boundary without appreciable migration of the original (sub)grain boundary (Figure 7.21a).

FIGURE 7.21. Recrystallization by (a) subgrain rotation and (b) grain boundary migration. In (a), a portion of a crystal is bounded by four tilt boundaries (ABCD); adding more dislocations of the same sign to the boundaries leads to progressively greater misorientation (i.e., a recrystallized grain). In (b), growth of a dynamically recrystallized grain occurs by bulging of the grain boundary into a neighboring grain with higher internal distortion (dark gray), leaving behind a relatively strain-free region that becomes a recrystallized grain. [9.29]

Eventually the crystallographic mismatch is sufficiently large that individual grains are recognized. Remember that progressive rotation of the subgrain occurs only by adding more dislocations in the boundary and that there is never loss of cohesion with the crystal lattice of the host grain. The convention we previously introduced to distinguish subgrains (low-angle grain boundaries) from recrystallized grains (high-angle grain boundaries) is an angle of 10°. This is admittedly an arbitrary convention, as we find a progression from low-angle to high-angle grain boundaries in rocks, but it is convenient for our description. Rotation recrystallization has been observed in most common rock-forming minerals, including calcite, quartz, halite, and olivine.

Migration recrystallization is a process by which grains grow at the expense of their neighbor(s)—when grain boundaries effectively sweep through neighbors. The grain that grows has a lower dislocation density than the grain(s) consumed. Let’s look at an example where the boundary of grain A migrates into grain B (Figure 7.21b). Keep in mind that a grain boundary separates two crystals whose lattices are not parallel. Migration happens when atoms in grain B near the boundary rearrange so they fit into the lattice of the crystal with lower dislocation density (grain A). As soon as this happens, these atoms become part of grain A. It is easier to rearrange atoms and bonds in grain B that are stretched and misoriented, because of its higher dislocation density. As the grain with lower dislocation density grows at the expense of the grain with higher dislocation density, the internal strain energy of the overall system decreases. Typically the boundary of the grain with lower dislocation density bulges into the grain with higher dislocation density (Figure 7.21b). Thus, this recrystallization process is also called bulge nucleation. When new grains deform as they grow, this may eventually arrest their growth. In natural settings, quartz, halite, and feldspar commonly recrystallize by bulge nucleation.

FIGURE 7.22. Core-mantle microstructure (or mortar structure). (a) Recrystallized grains occur at the edge of the mantle by progressive misorientation of subgrains. The internal portion of the host grain (core) shows weak deformation features such as undulose extinction and deformation bands, or may even be strain-free. (b) Photomicrograph of a core-mantle structure in deformed quartzite. Width of view is ~4mm. [9.30]

Recrystallized grains are best developed where large strain gradients exist, such as at grain boundaries. The common microstructure in which relatively deformation-free grain interiors progress to subgrains and then to recrystallized grains toward grain boundaries (Figure 7.22) is called a core-mantle structure or mortar structure. The importance of rotation recrystallization (subgrain rotation) and migration recrystallization (bulge nucleation) is largely a function of strain rate. Consider this: If you are in a hurry to get somewhere, you will try to take the fastest means of transportation. Similarly, nature uses the mechanism that produces the highest strain rate to reduce the internal strain energy of the system. Bulge nucleation is generally favored at higher strain rates and high temperatures. For both recrystallization mechanisms, the recrystallized grain size is inversely proportional to the strain rate. The smaller recrystallized grain size in mylonitic rocks, for example, is indicative of strain-rate increase. We observed work softening, strain-rate increase at constant stress, in some experiments, which can be understood in terms of the role of grainsize reduction during deformation.

Stress and Recrystallization

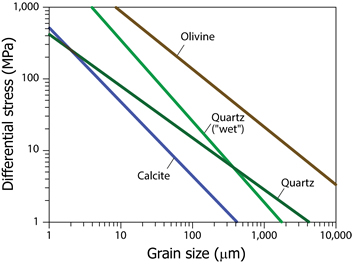
We saw that the formation of recrystallized grains is driven by the generation and motion of dislocations, which in turn is driven by differential stress. One can, therefore, expect that a relationship exists between recrystallized grain size and differential stress magnitude. Indeed, experiments have shown that a characteristic range of grain sizes occur for a specific condition of stress and mechanism of recrystallization. This means that we can potentially estimate paleostress conditions from microstructures; that is, recrystallized grain size can be used as a paleopiezometer. This is potentially a powerful tool for understanding the conditions of deformation in deep Earth, which cannot otherwise be obtained by direct measurements.

Although the debate about an exact relationship is not settled, it is generally agreed that recrystallized grain size is inversely proportional to differential stress magnitude

σd = A . d–i Eq. 7.7

where A and i are empirically derived parameters for a mineral and d is grain size in micrometers (μm). To give a rough idea of these relationships, we list representative parameters for three common minerals, calcite, quartz, and olivine below. When plotted (Figure 7.23), they illustrate the representative range of stress values from the study of naturally deformed rocks, such as mantle peridotites and quartz mylonites. In considering these values, remember that considerable uncertainty surrounds paleopiezometry. Overall, a small recrystallized grain size in a deformed rock reflects a high strain rate, a high differential stress magnitude, or a combination of both.

Mineral A (in MPa) i (d in μm)

Calcite 467 1.01

Quartz 381 0.71

Quartz (“wet”) 4090 1.11

Olivine 4808 0.79

From Mercier et al. (1977), Ross et al. (1980), Schmid et al. (1980), Ord and
Christie (1984).

FIGURE 7.23. Empirically derived recrystallized grain size versus differential stress relationships for calcite, quartz, “wet” quartz, and olivine, using the parameters listed. Note that we plot log σd versus log d, meaning that even small shifts in the position of each curve reflect significant changes in ambient conditions. [9.31]

Lastly, rock experiments show that the corresponding stress function during recrystallization has the form f(σ) = σn, so it is also called power-lap creep. The value of n, the stress exponent, varies, but typically lies in the range of 2 to 5 for common mono-mineralic rocks. We’ll return to this later.

DIFFUSIONAL MASS TRANSFER

Flow of rocks also occurs by the transfer of material through a process called diffusion. We’ll discuss three diffusion-related deformation mechanisms that are important for natural rocks, pressure solution, grain-boundary diffusion, and volume diffusion. We first examine the solid-state diffusion processes, followed by geometrically-similar, fluid-assisted diffusion, or pressure solution.

Diffusion occurs when an atom (or a point defect) migrates through a crystal. The process is strongly temperature dependent, because thermal energy causes atoms to vibrate, facilitating the breaking and reattachment of bonds. Increasing the temperature of a material proportionally increases the ability of individual atoms to jump to neighboring vacant sites. For example, at the melting temperature of Fe (Th = 1), the jump frequency, Γ, of vacancies is on the order of 1010 per second. The jump distance, r (the distance between atoms in the crystal structure), for each jump is 10–10 m (0.1 nm). We can determine the average area, R2, for a vacancy by Einstein’s equation:

R2 = Γ . t . r2 Eq. 7.8

where t = time. If we use t = 1 s, then R2 = 0.1 mm2, at Th = 1 for Fe metal. This area may seems small, so you might think at first that the process is relatively insignificant. However, considering that geologic time is in millions of years, the value of R2 becomes quite large. For example, at t = 1 m.y. (3.15 × 1013 s) the value of R2 is >3000 m2. Such large areas, however, are only representative for minerals in rocks near their melting temperature, which is not the typical condition during rock deformation. At lower Th, diffusion distances are orders of magnitude less. Another aspect of diffusion that needs to be appreciated is that R2 does not represent the linear distance between the original position of an atom and its position after time t. Diffusion is non-directional in an isotropic stress field; it is, what we call, a random-walk process. So, the final distance traveled is quite different from the total path or area covered.

Theoretical arguments, which we will not discuss here, define the diffusion coefficient, D, for a given mineral, describing movement of a species down a concentration gradient. The diffusion coefficient has the dimension area/time, which we can write in a form that includes the temperature dependence for diffusion and a minimum energy for migration to occur:

D = Do . exp(–E*/RT) Eq. 7.9

where Do is a material constant for diffusion that is empirically determined, E* is the activation energy for migration (kJ/mol), R is the gas constant (8.31 J/mol ⋅ K), and T is absolute temperature (in K). We present diffusivity in this particular form, because it is easier to compare with other constitutive equations for flow discussed later in this chapter. [Note: Strictly speaking equation 7.9 is for vacancy movement, and defines Dvac]

Grain-Boundary and Volume Diffusion

The two types of solid diffusion in crystals are grain-boundary diffusion, or Coble creep, and volume diffusion, or Nabarro-Herring creep. Mass transfer involving a reactive and transporting fluid phase, which is geometrically similar to grain-boundary diffusion, is called pressure solution (below). Given sufficient time, diffusing vacancies reach the surface of the crystal where they disappear. To see how this causes deformation, consider a crystal that is being subjected to a differential stress (Figure 7.24).

FIGURE 7.24. Diffusional flow by material transport through grains (volume diffusion or Nabarro-Herring creep) and on grain surfaces (grain-boundary diffusion or Coble creep), in response to differential stress (a), which results in shape change (strain) of the crystal (b). [9.20]

The vacancies migrate toward the site where stress is greatest and the atoms move to the sides where the stress is least. This results in an overall change in the distribution of mass, producing a change in shape of the crystal. But realize that this occurs without large-scale distortion of the crystal lattice. The diffusion of vacancies can occur through the entire body of a crystal or can be concentrated along a narrow region at its grain boundary (Figure 7.24a); both result in a permanent shape change as shown in Figure 7.24b. These deformation mechanisms are called volume diffusion (or Nabarro-Herring creep) and grain-boundary diffusion (or Coble creep), respectively. Thus, in the presence of a non-isotropic stress field we find that diffusion is directional.

Because both volume diffusion and grain-boundary diffusion produce strain by the movement of vacancies, the strain rate for each mechanism is a function of the diffusion coefficients (volume diffusion [Dv] and grain-boundary diffusion [Db] coefficients respectively), but also of the grain size (d):

ė (grain-boundary diffusion) ≅ Db/d2 Eq. 7.10

ė (volume diffusion) ≅ Dv /d3 Eq. 7.11

These simplified relationships emphasize the critical importance of grain size in diffusional creep: a larger grain size results in a less efficient process, so a lower strain rate. The activation energy for grain-boundary diffusion (included in Db) is less than that for volume diffusion (included in Dv), and the grain-size dependence of volume diffusion is larger. Thus, Coble creep is a more efficient process in crustal rocks than Nabarro-Herring creep, with the latter restricted to higher-temperature regions (e.g., temperatures in the deeper mantle) or to materials with very small grain sizes.

Pressure Solution

The somewhat misleading term pressure solution is used to describe a mass transfer process that occurs in natural rocks at temperatures much lower than those for solid diffusion as discussed above. The process is geometrically similar to grain-boundary diffusion, but involves the presence of a fluid film on grain boundaries. Pressure solution is important in crustal rocks because material transfer can occur at temperatures well below those required for solid diffusion, thanks to a chemically active fluid film that dissolves the crystal. The dissolved ions then move along a chemical gradient that arises from differential solubility in the presence of a differential (non-isotropic) stress to regions of deposition. Recall that fluids do not support shear stresses, so pressure solution only works if the fluid film is “attached” to the grain boundary by chemical bonds; thus, the fluid may not move, but dissolved atoms do.

Areas of high stress, say surfaces perpendicular to the maximum principal stress, exhibit enhanced solubility and the dissolved material is transported to regions under lower stress (surfaces perpendicular to the minimum principal stress). The geometric properties of the process are very similar to our earlier description of grain-boundary diffusion and, indeed, pressure solution produces shape changes like that in Figure 9.20b, except that it can occur at the low temperatures encountered near the Earth’s surface. A way to distinguish between these diffusional deformation mechanisms uses the terms fluid-assisted diffusion for pressure solution and solid-state diffusion for Nabarro-Herring creep and Coble creep; in colloquial terms we sometimes call them “wet diffusion” and “dry diffusion,” respectively.

FIGURE 7.25. Bedding-perpendicular pressure solution seams (stylolites) and veins (white structures) in argillaceous limestone Appalachians, Pennsylvania, USA). The middle bed is pure carbonate and does not contain as many seams. Note that the stylolites cut across bedding. Coin for scale. [9.21]

Because fluids are abundant in shallow crustal rocks and these have low ambient temperatures, pressure solution is an important deformation mechanism in upper crustal rocks. We infer the past activity of pressure solution diffusion in rocks from the presence of, for example, stylolites in limestones, grain overgrowths in sandstones, and cleavage and pressure shadows in some slates (Figure 7.25; see also Chapter 9). In contrast to dry diffusion, the distance over which material may be transported by fluid-assisted diffusion is not limited to individual grains, but can be substantial, particularly if the dissolved ions migrate into the pore fluid of the rock. Movement of pore fluid (i.e., groundwater flow) can flush the dissolved ions completely out of the rock, resulting in substantial volume loss. On the mesoscale, pressure solution may result in the formation of alternating layers of different composition, such as quartz-rich and mica-rich layers, in a process called differentiation. Alternatively, the dissolved ions may precipitate as vein fillings in cracks (Figure 7.25). The widespread occurrence of these pressure-solution structures in natural settings emphasizes the geologic importance of this deformation mechanism.

Analogous to grain-boundary diffusion, the strain rate associated with pressure solution is a function of the area and the rate of atoms that go into solution (i.e., the solubility of a material) in the fluid:

ė (pressure solution) ≅ Df/d2 Eq. 7.12

where Df is the diffusion coefficient of a phase that is dissolved in a fluid and d is the grain size.

Superplasticity

The efficiency of diffusion processes in high-temperature environments results in grain-boundary sliding superplasticity (GBSS), less cumbersomely called superplastic creep. Let’s look at the characteristics first. Superplastic creep is a grain size-sensitive deformation mechanism in which a body changes shape through grains sliding past one another. At first this may sound like cataclastic flow that we discussed in the Frictional Regime, but there is an important distinction. In superplastic creep, volume and grain-boundary diffusion are sufficiently efficient to keep gaps from forming between moving grains, and therefore grains are able to slide without friction. Strain is produced by something we call neighbor switching, as illustrated in Figure 7.26.

FIGURE 7.26. Superplastic creep. Neighbor switching occurs in a group of four grains that enjoy ∼55% strain with little deformation of each grain, except diffusional modification of the boundaries to accommodate grain sliding (small arrows). [9.32]

Superplastic creep can result in very large strains (>1,000%) without appreciable internal deformation of the grains. The original definition of superplasticity is, in fact, this ability of rocks to accumulate very large strains without mesoscopic breaking. Even after large finite strains, grains are equiaxial and “fresh-looking,” and show no preferred elongation or crystallographic fabric. This diffusion-assisted mechanism is mainly important in materials with relatively small grain sizes (<15 μm) that facilitate diffusion. In this context, recall Equations 7.9 and 7.10, which show the inverse exponential proportionality of diffusion to grain size.

Superplastic creep has been proposed as a natural deformation mechanism in fine-grained calcite- and quartz-rich rocks. The very high temperatures that occur in the mantle would also permit this mechanism in coarser-grained olivine-rich rocks. Superplastic creep occurs at lower differential stresses than dislocation creep, but it requires rocks with relatively small grain sizes. Thus, a rock may initially deform by dynamic recrystallization until its grain size is sufficiently reduced for superplastic creep to occur. When this happens, the rock becomes much weaker; meaning, the stress necessary to produce strain decreases. This weakening, known as work or strain softening, is common in mid-crustal and deeper fault zones.

The stress function of the flow law for superplasticity approaches linearity between strain rate and stress; that is, the stress component n approaches 1. Consequently, the strain rate is inversely proportional to grain size:

ė (superplasticity) ≅ d–r Eq. 7.13

where r is 2 to 3 based on experimental work. Recalling that a linear relationship between strain rate and stress defines linear viscous rheology (Chapter 5), superplastic creep is well described by Newtonian fluid mechanics. This contrasts with dislocation creep, which typically has nonlinear rheology (n ≠ 1). To emphasize the strong grain-size dependence of superplastic creep, it is also called grain-size-sensitive creep.

DEFORMATION MECHANISM MAPS

Quite an array of concepts and terms have by now been introduced, so let’s attempt to create, out of this information, a pattern that helps you to remember the important elements and relationships. The activity of ductile deformation mechanisms can be summarized in a diagram that shows over what ranges of stress, strain rate, temperature, and grain size each mechanism dominates for a given material; such diagrams are called deformation mechanism maps.

FIGURE 7.27. Schematic of a deformation mechanism map, showing normalized stress versus homologous temperature at constant grain size. [9.33]

The variables may be stress (e.g., differential stress), temperature, and grain size, but for comparison between different materials we generally use normalized parameters. A normalized physical quantity is the ratio between a variable and a material constant measured in the same units. In this case, stress is normalized to an elastic modulus of the material (typically the shear modulus, G), and temperature (absolute temperature, in K) is normalized to the absolute melting temperature of the material (Figure 7.27), the homologous temperature, Th.

FIGURE 7.28. Deformation mechanism map for olivine with a grain size of 100 μm. Variables are the same as in Figure 9.33, except that depth is substituted for temperature, using an exponentially decreasing geothermal gradient with 300K at the surface and 1850K at 500 km depth. (From Ashby and Verrall, 1978) [9.36]

On the deformation mechanism map we display lines of constant strain rate, as shown in Figures 9.36. Whereas only a small region of the diagram can be constrained by laboratory experiments, we must extrapolate to most natural conditions. This is comparatively easy where an essentially linear (Newtonian) relationship exists between ė and σ, such as for diffusional flow. For other regimes, such as dislocation glide (exponential-law creep), and dislocation glide and climb (power-law creep), the extrapolation of these nonlinear relationships is more tenuous.

The meaning of boundaries between the fields on a deformation mechanism map is not straightforward, because deformation mechanisms do not change abruptly at this boundary; rather, several mechanisms operate simultaneously. The mechanism that generates the highest strain rate is the dominant deformation mechanism. Fields in deformation mechanism maps are defined by calculating the strain rate for each mechanism. Then, the mechanism giving the fastest rate is taken as dominant for a field. For example, the field for dislocation creep represents the range of conditions for which dislocation glide creates a strain rate faster than any other mechanism, even though these other mechanisms may be operating. This means that at a boundary the two adjacent deformation mechanisms are equally important. Let’s have a practical example. During mylonitization of a quartzite, dynamic recrystallization may dominate; yet diffusional flow may occur simultaneously if the grain size and the strain rate are sufficiently small. Consequently, the map will indicate that we are in the power-law field, but we also see microstructural evidence for diffusional flow.

We illustrate a general pattern that is common to all deformation mechanism maps, with the mineral olivine that is a representative material for (upper) mantle rocks (Figure 7.28). Instead of homologous temperature we plot depth in Earth, based on a thermal gradient that exponentially decreases from 300K at the surface to 1850K at a depth of 500 km. This enables us also to take into account any effects of pressure, which play a role in the mantle by increasing the flow strength and decreasing the strain rate. From the olivine deformation mechanism map you see that cataclastic flow and exponential-law creep are restricted to relatively large differential stresses (here ≈ 8 × 102 MPa), meaning that these mechanisms are limited to shallow crustal levels. With depth, we pass from exponential-law creep to power-law creep to diffusional creep, given a constant geologic strain rate (say, 10–14/s). In the latter regime, we may pass from grain-boundary diffusion (Coble creep) to volume diffusion (Nabarro-Herring creep), given further temperature or strain-rate change.

The power of a deformation mechanism map lies in its ability to predict the mechanism that dominates flow under natural conditions. For example, if we assume that the Earth’s upper mantle consists mainly of olivine, we predict that, at strain rates greater than 10–11/s, dislocation glide and climb dominate flow in the upper 100 km, given an average grain size of 100 μm. If the strain rate is less, diffusional creep will be more important, especially when the grain size is small. The latter point, the effect of grain size, may not be clear from any of the deformation mechanism maps shown thus far, because grain size was taken as constant value. So how do we include the role of grain-size? Revisit the flow laws for diffusional creep (Equation 9.15), which state that strain rate is inversely proportional to the square or cube of the grain size. Reducing grain size by, say, one order of magnitude will increase strain rate by two to three orders of magnitude, which will move deformation at reasonable geologic strain rates into the fields of diffusional flow. Similarly, if we construct a map for a grain size of, say, 1 mm (1000 μm) or larger, the deformation at geologic strain rates moves into the field of power-law creep. With grain sizes for upper-mantle olivine in the range of 100–1000 μm, the microstructures of mantle rocks generally support the predictions that we obtain from olivine deformation-mechanism maps.

Applications and Limits

Deformation mechanism maps can be constructed for all types of material behavior, not restricted to rocks. For example, they give predictions of the deformation of metal in a nuclear reactor, thereby aiding their safe design; they can determine the lifespan of lightbulb filaments; they explain the creep of ice sheets. So, deformation mechanism maps are a powerful approach to understanding and exploring the rheology of materials, and to applying this information to significant Earth science problems such as shear zones, mantle convection or subduction. However, these maps are not without limitations.

First, extrapolation over several orders of magnitude is needed to move from experimentally-derived flow laws (ė > 10–8/s) to geologic conditions (ė < 10–12/s), introducing a major source of uncertainty. We’ll return to this in the chapter on lithosphere rheology. Second, deformation-mechanism maps assume steady-state flow (meaning that stress is strain-independent), which may not be sufficiently representative of geologic conditions. Thirdly, evolving microstructures affect the dominant deformation mechanism; for example, dynamic recrystallization tends to reduce the grain size, which in turn enhances the importance of diffusional creep and weakens the material. In spite of these limitations, deformation mechanism maps are a handy and powerful tool to evaluate and predict deformation mechanisms and extract conditions for deforming materials in Earth. Comparison of natural deformation structures with predictions based on deformation mechanism maps offers a natural test, which indicate that the maps provide reliable estimates on the conditions of deformation.

CONFUSING TERMINOLOGY?

Deformation Behaviors, Mechanisms and Regimes

You will find that a range of terms is variably used in the literature to describe the response of materials to stress and the formation of geologic structures, some of which with different meanings depending on the community. For example, the term ductile is used to describe distributed strain in structural geology, but also as a synonym for crystal plasticity in geophysics. We use these definitions:

• Behavior. How does a material respond to stress? Does it localize deformation, like breaking of a plate, or distributed deformation, like reshaping of soft clay. The terms brittle and ductile describe these behaviors, respectively.

• Mechanism. What processes dominate? Is material moving along a fault, representing frictional sliding, or, flowing, like a glacier or mylonite, by crystal plasticity.

• Regime. What are the ambient conditions during deformation? Is pressure the dominant environmental parameter, resulting in frictional processes, like faulting and sliding. Or is temperature dominant, promoting crystal plastic and diffusional processes, like a salt glacier in the upper crust, formation of mylonites in deeper crust, or flow of mantle rocks.

Figure 7.29. Deformation experiment with two cubes containing marbles (a), and balls of clay (b), showing ductile strain accumulation by different deformation mechanisms. The finite strain is equal in both cases and the mode of deformation on the scale of the block is distributed (ductile behavior). However, the mechanism by which the deformation occurs is quite different: in (a) frictional sliding of undeformed marbles occurs, while in (b) individual clay balls distort into ellipsoids. [5.19]

The distinction between mechanisms and behaviors can be illustrated by a simple experiment (Figure 7.29). Consider a cube that is filled with small undeformable spheres (e.g., marbles) and a second cube that is filled with spheres consisting of clay. If we deform these cubes into rectangular blocks, the mechanism by which this shape change is achieved is very different. In Figure 7.29a, the rigid spheres slide past one another to accommodate the shape change without distortion of the individual marbles; a process called cataclastic flow. In Figure 7.29b, the shape change is achieved by changes in the shape of individual clay balls to ellipsoids. In both cases the deformation is not localized, but distributed throughout the block, at the sphere boundaries in Figure 7.29a and within the spheres in Figure 7.29b. Both experiments are therefore expressions of ductile behavior, although the mechanisms by which strain accumulated are quite different.

Brittle and Ductile Behavior

FIGURE 7.30. Brittle (a) to brittle-ductile (b) to ductile (c) deformation, reflecting the distinction between degrees of localized and distributed strain. [5.21]

As we noted, you will find that the terms brittle and ductile and are variably used, so, in closing, we define them here more strictly as behaviors (Figure 7.30):

• Brittle. The response of a solid material to stress during which it loses continuity (cohesion). Brittle behavior reflects the role of fracture mechanisms where strain is localized. It occurs when stresses exceed a critical value (failure stress), after a body has undergone elastic (+/- minor viscous) strain.

• Ductile. The response of a solid material to stress such that it flows like a fluid. In a material that deforms ductilely, strain is distributed, meaning that it accumulates without the formation of mesoscopic discontinuities. Ductile behavior can involve both brittle and plastic deformation, as shown in the experiment above (Figure 7.29).

• Brittle-Ductile. The transitional stage where strain is distributed (ductile), but also localized (brittle) in places. Whereas it is sometimes used as a synonym for frictional-plastic transition, we distinguish behavior from mechanism.

Back to The Plastic Regime Contents

Back to PSG&T Home

v1.4; Last update: 15-sep-23

[1] Named after the English physicist Isaac Newton (1642–1727).

[2] by Sir Charles Lapworth in the late 1900s