We frequently use the words force and stress in casual conversation. Stress from yet another deadline, a test, or maybe an argument with a roommate or spouse. Appropriate force is applied to reach our goal, and so on. In science, however, these terms have very specific meanings. For example, the force of gravity keeps us on the Earth’s surface and the force of impact destroys our car. Like us, rocks experience the pull of gravity, and forces arising from plate interactions result in a range of geologic structures, from microfabrics to mountain ranges (Figure 2.1). Dynamic analysis, the study of stresses in a body, is a topic whose relevance goes well beyond structural geology. Societal challenges like building collapse and mass wasting come to mind as examples of phenomena whose disastrous effects can be minimized by adequate knowledge of stress states.

FIGURE 2.1. Aerial view of the Karakoram range of the Himalaya (northern Pakistan). (https://goo.gl/EGLjbU)

In this chapter we begin with the fundamentals of force and stress, followed by a look at the components of stress that eventually produce tectonic structures. In later chapters we will use these concepts to examine the relationship between geological structures and stress, and tectonics.

2.2 Mechanics

To understand tectonic processes we must be familiar with the fundamental principles of mechanics. Mechanics is concerned with the action of forces on bodies and their effect; you can say that mechanics is the science of motion. Newtonian [1] (or classical) mechanics studies the action of forces on rigid bodies. The equations of Newtonian mechanics adequately describe a range of movements in the natural world, from the entertaining interaction between colliding balls at a game of pool (Figure 2.2a) to the galactic dance of the planets in our solar system. When reaching the subatomic level, Newtonian mechanics starts to break down and we enter the complex realm of quantum mechanics.

FIGURE 2.2. The interaction of non-deformable bodies is described by Newtonian (or classical) mechanics (a) and that between deformable bodies by continuum mechanics (b). Imagine the difference between playing pool with regular balls and balls made of jelly.

In tectonic structures we commonly deal with interactions that involve not only movement, but also distortion; material displacements occur both between and within bodies. Imagine playing pool with balls made up of jelly rather than solids (Figure 2.2b). The theory associated with this type of behavior is the focus of continuum mechanics. In continuum mechanics, a material is treated as a continuous medium (hence the name), that is, there are no discontinuities that appreciably affect its behavior. This may seem inappropriate for rocks at first, because we know that they consist of grains whose boundaries are material discontinuities by definition. Yet, on the scale of a rock body containing thousands or more grains we may consider the system statistically homogeneous. Indeed, the predictions from continuum mechanics theory give us adequate first order descriptions of displacements in many natural rocks. The primary reason to use the simplifications of continuum mechanics is that it provides us with a mathematical description of deformation in relatively straightforward terms. When the behavior of rocks is dominated by discrete discontinuities, like fractures, continuum mechanics theory no longer holds. Then we need to resort to more complex modeling methods that fall outside the scope of this book.

By the time you have reached the end of this chapter, a good number of terms and concepts will have appeared. For convenience and future reference, therefore, some of the more common terms are listed in Supplementary Materials of this unit.

2.2.1 Units and Fundamental Quantities

When measuring something you must select a unit for the quantity that is to be measured. The physical properties of a material can be expressed in terms of four fundamental quantities: mass, length, time, and charge. For our purposes we can ignore the quantity charge, which describes the electromagnetic interaction of particles. It plays a role, however, when we try to understand the behavior of materials at the atomic scale. The units of mass, length, and time are the kilogram (kg), the meter (m), and the second (s), respectively. This notation follows the Système International (French), better known as SI units. Throughout the text we will use SI units, but other conventions remain popular in geology (such as “kilobar,” which is a measure of pressure). Where appropriate we will add these units in parentheses. In Table 3.2 the SI units of stress and some common conversions are given. The symbol for mass is [m], for length [l], and for time [t]. Velocity [v], which combines the fundamental quantities of length and time, has the units of length divided by time. In conventional symbols this is written as:

[v] : [lt –1]

in which the colon means “has the quantity of.” Such dimensional analysis is a check on the relevance of an equation. We begin by using it in the case of a force.

2.2.2 Force

Kicking or throwing a ball shows that a force changes the velocity of an object. Newton’s first law of motion, also called the Law of Inertia, says that in the absence of a force a body moves either at constant velocity or is at rest. Stated more formally: a free body moves without acceleration. Change in velocity is called acceleration [a], which is defined as velocity divided by time:

[a] : [v.t –1] : [lt –2]

The unit of acceleration, therefore, is m/s2.

Force [F], according to Newton’s Second Law of Motion, is mass multiplied by acceleration

F = m. a

with the quantities:

[F] : [m.a] : [mlt–2]

The unit of force is kg ⋅ m/s2, called a newton (N) in SI units. You can feel the effect of mass when you throw a tennis ball and a basketball and notice that a different force is required to move each of them. Force, like velocity, is a vector quantity, meaning that it has both magnitude and direction. So it can be graphically represented by a+++ line with an arrow on one side. Manipulation of forces conforms to the rules of vector algebra. For example, a force at an angle to a given plane can be geometrically resolved into two components; say, one parallel and one perpendicular to that plane.

Natural processes can be described with four basic forces: (1) the gravity force, (2) the electromagnetic force, (3) the nuclear or strong force, and (4) the weak force. Gravity is a force that acts over large distances and is always attractive; for example, the ocean tides reflect the gravitational interaction between the Moon and the Earth. The other three forces act only over short ranges (atomic scale) and can be attractive or repulsive. The electromagnetic force describes the interaction between charged particles, such as the electrons around the atomic nucleus; the strong force holds the nucleus of an atom together; and the weak force is associated with radioactivity. It is quite possible that only one fundamental force exists in nature, but, despite the early efforts of Albert Einstein [2] and much progress since then, it has not so far been possible to formulate a Grand Unified Theory to encompass all four forces. The force of gravity has proved to be a particular problem.

Forces that result from action of a field at every point within the body are called body forces. Bungee jumping gives you a very vivid sensation of body forces though the action of gravity. The magnitude of body forces is proportional to the mass of the body. Forces that act on a specific surface area in a body are called surface forces. They reflect the pull or push of the atoms on one side of a surface against the atoms on the other side. Examples are a cue stick’s force on a pool ball, the force of expanding gases on an engine piston, and the force of the jaws of a vice. The magnitude of surface forces is proportional to the area of the surface. Forces that act on a body may change the velocity of (that is, accelerate) the body, and/or may result in a shape change of the body, meaning acceleration of one part of the body with respect to another part. Although force is an important concept, it does not distinguish the effect of an equal force on bodies of equal mass but with different shapes. Imagine the effect of the same force applied to a sharp object and a dull object. For example, a human is comfortably supported by a water bed, but when you place a nail between the person and the water bed, the effect is quite dramatic. Using a more geologic experience, consider hitting a rock with a pointed or a flat hammer using the same force. The rock cracks more easily with the pointed hammer than with the flat-headed hammer; in fact, we apply this principle when we use a chisel rather than a sledge hammer to collect rock samples. These examples of the intensity of force lead us into the topic of stress.

2.3 STRESS

Stress, represented by the symbol σ (sigma), is defined as the force per unit area [A]:

σ = F/A Eq. 2.1

You can, therefore, consider stress as the intensity of force, or a measure of how concentrated a force is. A given force acting on a small area (the pointed hammer mentioned previously) will have a greater intensity than that same force acting on a larger area (a flat-headed hammer), because the stress associated with the smaller area is greater than that with the larger area. Those of you remembering turntables and vinyl records (ask your parents) are familiar with this effect. The weight of the arm holding the needle is only a few grams, but the stress of the needle on the vinyl record is orders of magnitude greater because the contact area between needle and record is very small. The high stresses at the area of contact eventually gave rise to scratches and ticks in the records, so it is little wonder that we have embraced digital technologies.

You will see that stress is a complex topic, because its properties depend on the reference system. Stress that acts on a plane is a vector quantity, called traction, whereas stress acting on a body is described by a higher order entity, called a stress tensor. In the next few pages we will gradually develop the pertinent concepts and components of stress. Because stress is force per unit area it is expressed in terms of the following fundamental quantities:

[σ] : [mlt–2 ⋅ l–2] or [ml–1 ⋅ t–2]

The corresponding unit of stress is kg/m ⋅ s2 (or N/m2), which is called a pascal (Pa)[3]. Instead of this SI unit, however, many geologists continue to use the unit bar, which is approximately 1 atmosphere. These units are related as follows:

1 bar = 105 Pa ≈ 1 atmosphere

In geology you will generally encounter their larger equivalents, the kilobar (kbar) and the megapascal (MPa):

1 kbar = 1000 bar = 108 Pa = 100 MPa

The unit gigapascal (1 GPa = 1000 MPa = 10 kbar) is used to describe the very high pressures that occur deep in Earth. For example, the pressure at the core-mantle boundary, located at a depth of approximately 2900 km, is ∼135 GPa, and at the center of the Earth (at a depth of 6370 km) the pressure exceeds 350 GPa. Later we will see how these values can be calculated.

2.3.1 2D Stress: Normal Stress and Shear Stress

Stress acting on a plane is a vector quantity, meaning that it has both magnitude and direction; it is sometimes called traction. Stress on an arbitrarily oriented plane, however, is not necessarily perpendicular to that plane, but, like a vector, it can be resolved into components normal to the plane and parallel to the plane (Figure 2.3).

FIGURE 2.3. The stress on a two-dimensional plane is defined by a stress acting perpendicular to the plane (the normal stress) and a stress acting along the plane (the shear stress). The normal stress and shear stress are perpendicular to one another.

The vector component normal to the plane is called the normal stress, for which we use the symbol σn (sometimes just the symbol σ is used); the vector component along the plane is the shear stress and has the symbol σs (sometimes the symbol τ (tau) is used for σs). In contrast to the resolution of forces, the resolution of stress into its components is not straightforward, because the area changes as a function of the orientation of the plane with respect to the stress vector. Let us first examine the resolution of stress on a plane in some detail, because, as we will see, this has important implications.

In Figure 2.4, stress σ has a magnitude F/AB and makes an angle θ with the top and bottom of our square. The forces perpendicular (Fn) and parallel (Fs) to the plane EF are:

Fn = F cos θ = σ AB cos θ = σ EF cos2 θ

(AB = EF cos θ) Eq. 2.2

Fs = F sin θ = σ AB sin θ =

σ EF sin θ cos θ = σ EF 1⁄2(sin 2θ) Eq. 2.3

Thus the corresponding stresses are:

σn = Fn/EF = σ cos2 θ Eq. 2.4

σs = Fs/EF = σ 1⁄2(sin 2θ) Eq. 2.5

FIGURE 2.4. The relationship between force (F) and stress (σ) on a plane. Section through a cube showing face ABCD with ribs of length AB on which a force F is applied. This force is resolved into orientations parallel (Fs) and perpendicular (Fn) to a plane that makes an angle θ with the top and bottom surface (EF is the trace of this plane). The magnitudes of vectors Fs and Fn are a function of the angle θ: Fn = F ⋅ cos θ, Fs = F ⋅ sin θ. The magnitude of the normal (σn) and shear stress (σs) is a function of the angle θ and the area: σn=σcos2 θ, σs=σ 1⁄2 (sin 2θ). (a) Force F on plane; (b) stress σ on plane; (c) normalized values of Fn and σn on plane with angle θ; (d) normalized values of Fs and σs on a plane with angle θ.

You notice that the equation for the normal stress and the normal force are different, as are the equations for Fs and σs. We graphically illustrate this difference between forces and stresses on an arbitrary plane by plotting their normalized values as a function of the angle θ in Figure 2.4c and 2.4d, respectively. In particular, the relationship between Fs and σs is instructive for gaining an appreciation of the area dependence of stress. Both the shear force and the shear stress initially increase with increasing angle θ; at 45° the shear stress reaches a maximum and then decreases (recall the y=sin2x curve), while Fs continues to increase. Thus, the stress vector acting on a plane can be resolved into vector components perpendicular and parallel to that plane, but their magnitudes vary as a function of the orientation of the plane. Let us further examine the properties of stress by determining the stress state for a three-dimensional body.

2.3.2 3D Stress: Principal Planes and Principal Stresses

Previously, we discussed stress acting on a single plane (the two-dimensional case), recognizing two vector components, the normal stress and the shear stress. However, to describe stress on a randomly oriented plane in space we need to consider the three-dimensional case. We limit unnecessary complications by setting the condition that the body containing the plane is at rest. So a force applied to the body is balanced by an opposing force of equal magnitude but opposite sign; this condition is known as Newton’s Third Law of Motion. Using another Newtonian sports analogy, kick a ball that rests against a wall and notice how the ball (the wall, in fact) pushes back with equal enthusiasm.

2.3.3 The Components of 3D Stress

The orientation and magnitude of the stress state of a body is defined in terms of its components projected in a Cartesian reference frame, which contains three mutually perpendicular coordinate axes, x, y, and z. To see this, instead of a point representing an infinite number of planes on which our stress acts, we draw our point as an infinitely small cube whose ribs are perpendicular to each of the coordinate axes, x, y, and z. Why a cube? A cube is a 3D object with the least number of unique planes (three). We resolve the stress acting on each of the three unique faces of a cube into three components (Figure). For a face normal to the x-axis the components are σxx, which is the component normal to that face, and σxy and σxz, which are the two components parallel to that face. These last two stresses are shear stress components, acting along one of the other coordinate axes y and z, respectively.

FIGURE 2.5. Resolution of stress into components perpendicular (three normal stresses, σn) and components parallel (six shear stresses, σs) to the three faces of an infinitesimally small cube, relative to the reference system x, y, and z.

Applying this same procedure for the faces normal to y and z, we obtain a total of nine stress components (Figure 2.5):

In the direction of: x: y: z:

stress on the face normal to x: σxx σxy σxz

stress on the face normal to y: σyx σyy σyz

stress on the face normal to z: σzx σzy σzz

The columns, from left to right, represent the components in the x, y, and z directions of the coordinate system, respectively. σxx, σyy, and σzz are normal stress components and the other six are shear stress components. Because we specified that the body itself is at rest, three of the six shear stress components must be equivalent (σxy and σyx, σyz and σzy, and σxz and σzx). If these components were unequal, the body would move, which violates our at-rest condition. So, rather than nine components, we are left with six independent stress components to describe the stress acting on any arbitrary infinitesimal body:

In the direction of:x: y: z:

stress on the face normal to x: σxxσxy σxz

stress on the face normal to y: σxy σyy σyz

stress on the face normal to z: σxz σyz σzz

The only ingredient left in our description is a sign convention. In physics and engineering, tensile stress is considered positive, and compressive stress negative. In geology, however, it is customary to make compression positive and tension negative, because compression is more common in the Earth. We will, therefore, use the geologic sign convention throughout the text; however, don’t confuse this with the engineering sign convention used in some other textbooks.

For any given state of stress there is at least one set of three mutually perpendicular planes on which the shear stresses are zero. In other words, you can rotate our infinitesimal cube such that the shear stresses on each of its three faces are zero. In this orientation, these three faces are the principal planes of stress (the same ones that we described in the stress ellipsoid; below) and they intersect in three mutually perpendicular axes that are the principal axes of stress (which are the axes of the stress ellipsoid; below). The stresses acting along them are called the principal stresses for a given point or homogeneous domain within a body.

2.3.4 The Stress Ellipsoid

We shrink our three-dimensional body containing the plane of interest down to the size of a point for our analysis of the stress state of an object. Why this seemingly obscure transformation? Recall that two nonparallel planes have a line in common and that three or more nonparallel planes have a point in common. In other words, a point defines the intersection of an infinite number of planes with different orientations. The stress state at a point, therefore, can describe the stresses acting on all planes in a body.

FIGURE 2.6. (a) A point represents the intersection of an infinite number of planes, and the stresses on these planes describe an ellipse in the two-dimensional case. In three dimensions this stress envelope is an ellipsoid (b), defined by three mutually perpendicular principal stress axes (σ1≥σ2≥σ3). These three axes are normal to the principal planes of stress.

In Figure 2.6a the normal stresses (σ) acting on four planes (a–d) that intersect in a single point are drawn. For clarity, we limit our illustrations to planes that are all perpendicular to the surface of the page, allowing the use of slice through the body. You will see later that this geometry easily expands into the full three-dimensional case. Because of Newton’s Third Law of Motion, the stress on each plane must be balanced by one of opposite sign (σ = –σ). Because stress varies as a function of orientation, the magnitude of the normal stress on each plane (represented by the vector length) is different. If we draw an envelope around the end points of these stress vectors (red line in Figure 6a), we obtain an ellipse. Recall from geometry that an ellipse is defined by at least three non-perpendicular axes. This means that the magnitude of the stress for all possible planes is represented by a point on this stress ellipse. Now, the same can be done in three dimensions, but this is hard to illustrate on a piece of flat paper. Doing the same analysis in three dimensions, we obtain an envelope that is the three-dimensional equivalent of an ellipse, called an ellipsoid (Figure 2.6b). This stress ellipsoid fully describes the stress state at a point and enables us to determine the stress for any given plane. Like all ellipsoids, the stress ellipsoid is defined by three mutually perpendicular axes, which are called the principal stresses. These principal stresses have two properties: (1) they are orthogonal to each other, and (2) they are perpendicular to three planes that do not contain shear stresses; these planes are called the principal planes of stress. So, we can describe the stress state of a body simply by specifying the orientation and magnitude of three principal stresses.

2.4 DERIVING KEY STRESS RELATIONSHIPS

Now that we can express the stress state of a body by its principal stresses, we can derive several useful relationships. Let’s carry out a simple classroom experiment in which we compress a block of clay between two planks (Figure 2.7). As the block of clay develops a fracture, we want to determine what the normal and the shear stresses on the fracture plane are. To answer this question our approach is similar to our previous one (Equations 2.2 to 2.5), but now we express the normal and shear stresses in terms of the principal stress axes.

FIGURE 2.7. Determining the normal and shear stresses on a plane in a stressed body as a function of the principal stresses. For a classroom experiment, a block of clay is squeezed between two planks of wood. AB is the trace of fracture plane P in our body that makes an angle θ with σ3. The two-dimensional case shown is sufficient to describe the experiment, because σ2 equals σ3 (atmospheric pressure).

The principal stresses acting on our block of clay are σ1 (maximum stress), σ2 (intermediate stress), and σ3 (minimum stress). Since we carry out our experiment under atmospheric conditions, the values of σ2 and σ3 will be equal, and we may simplify our analysis by neglecting σ2 and considering only the σ1-σ3 plane, as shown in Figure X. The fracture plane makes an angle θ (theta) with σ3. This plane makes the trace AB in Figure X, which we assign unit length (that is, 1) for convenience. We can resolve AB along AC (parallel to σ1) and along BC (parallel to σ3). Then, by trigonometry, we see that the area represented by AC = sin θ, and the area represented by BC = cos θ. Note that if we assign dimension L to AB then AC = L ⋅ sin θ and BC = L ⋅ cos θ.

Next we consider the forces acting on each of the surface elements represented by AB, BC, and AC. Since force equals stress times the area over which it acts, we obtain:

force on side BC = σ1 ⋅ cos θ

force on side AC = σ3 ⋅ sin θ

The force on side AB consists of a normal force (i.e., σn ⋅ 1) and a shear force (i.e., σs ⋅ 1); recall that force is stress times area.

For equilibrium, the forces acting in the direction of AB must balance, and so must the forces acting perpendicular to AB (which is parallel to CD). Hence, resolving along CD:

force ⊥ AB = force ⊥ BC resolved on CD +

force ⊥ AC resolved on CD

1 ⋅ σn = σ1 cos θ ⋅ cos θ + σ3 sin θ ⋅ sin θ Eq. 2.6

σn = σ1 cos2 θ + σ3 sin2 θ Eq. 2.7

Substituting these trigonometric relationships in Equation 2.7, we obtain:

cos2 θ = 1⁄2(1 + cos 2θ)

sin2 θ = 1⁄2(1 – cos 2θ)

simplifying gives:

σn = 1⁄2(σ1 + σ3) + 1⁄2(σ1 – σ3) cos 2θ Eq. 2.8

and

force parallel AB = force ⊥ BC resolved on AB +

force ⊥ AC resolved on AB

1 ⋅ σs = σ1 cos θ ⋅ sin θ – σ3 sin θ ⋅ cos θ Eq. 2.9

Note that the force perpendicular to AC resolved on AB acts in a direction opposite to the force perpendicular to BC resolved on AB, hence a negative sign is needed in Eq. 2.9, which further simplifies to:

σs = (σ1 – σ3) sin θ ⋅ cos θ Eq. 2.10

Substituting this trigonometric relationship in Eq. 2.109, we get:

sin θ ⋅ cos θ = 1⁄2 sin 2θ

which gives:

σs = 1⁄2(σ1 – σ3) sin 2θ Eq. 2.11

From Equations 2.8 and 2.11 we can determine that the planes of maximum normal stress are at an angle θ of 0° with σ3, because cos 2θ reaches its maximum value (cos 0° = 1). Secondly, planes of maximum shear stress lie at an angle θ of 45° with σ3 because sin 2θ reaches its maximum value (sin 90° = 1) (see also Figure 2.4c and d). Whereas faulting resulted in a shearing motion along the fault plane, we find that the fault plane in our experiment is not parallel to the plane of maximum shear stress (θ > 45°). This perhaps surprising result reflects a fundamental property of solids that we further examine in Chapter 3.

2.5 MOHR DIAGRAM FOR STRESS

The equations we derived for σn and σs do not offer an obvious sense of their values as a function of orientation of a plane in our block of clay. Of course, a programmable calculator or simple computer program (spreadsheet) will do the job, but a convenient graphical method, known as the Mohr diagram [4] (Figure 2.8), was introduced over a century ago to solve Equations 2.8 and 2.11.

FIGURE 2.8. The Mohr diagram for stress. Point P in this construction represents the plane in our experiment of Figure 7.

A Mohr diagram is an “XY”-type (Cartesian) plot of σs versus σn that graphically solves the equations for normal stress and shear stress acting on a plane within a stressed body. In our experiences, many people find the Mohr construction difficult to comprehend. So we’ll first examine the proof and underlying principles of this approach to try to take the magic out of this powerful graphic method.

If we rearrange Equations 2.8 and 2.11 and square them, we get:

[σn – 1⁄2(σ1 + σ3)]2 = [1⁄2(σ1 – σ3)]2 cos2 2θ Eq. 2.12

σs2 = [1⁄2(σ1 – σ3)]2 sin2 θ Eq. 2.13

Adding Equations 2.12 and 2.13 gives:

[σn – 1⁄2(σ1 + σ3)]2 + σs2 =

[1⁄2(σ1 – σ3)]2 ⋅ (cos2 2θ + sin2 2θ) Eq. 2.14

Using the trigonometric relationship (cos2 2θ + sin2 2θ) = 1 in Equation 2.14 gives:

[σn – 1⁄2(σ1 + σ3)]2 + σs2 = [1⁄2(σ1 – σ3)]2 Eq. 2.15

Observe that Equation 2.15 has the form (x – a)2 + y2 = r2, which is the general equation for a circle with radius r and centered on the x-axis at distance a from the origin. Thus the Mohr circle has a radius 1⁄2(σ1 – σ3) that is centered on the σn axis at a distance 1⁄2(σ1 + σ3) from the origin. The construction is shown in Figure X. You also see from this figure that the Mohr circle’s radius, 1⁄2(σ1 – σ3), is the maximum shear stress, σs, max. The stress difference (σ1 – σ3), called the differential stress, is indicated by the symbol σd.

2.5.1 Constructing the Mohr Diagram

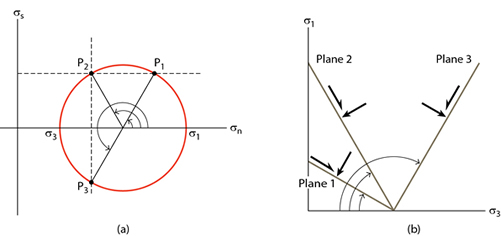
To construct a Mohr diagram we draw two mutually perpendicular axes; σ is the abscissa (x-axis) and σs is the ordinate (y-axis). In our clay deformation experiment, the maximum principal stress (σ1) and the minimum principal stress (σ3) act on plane P that makes an angle θ with the σ3 direction; in the Mohr construction we then plot σ1 and σ3 on the σn-axis (Figure X). These principal stress values are plotted on the σn axes because they are normal stresses, but with the special condition that the planes on which they act, the principal planes, have zero shear stress (σs = 0). We then construct a circle through points σ1 and σ3, with O, the midpoint, at 1⁄2(σ1 + σ3) as center, and a radius of 1⁄2(σ1 – σ3). Next, we draw a line OP such that angle POσ1 is equal to 2θ. This step often gives rise to confusion and errors. First, remember that we plot twice the angle θ, which is the angle between the plane and σ3, because of the equations we are solving. Second, we measure 2θ from the σ1-side on the σn-axis. Why? Consider a plane with θ=0 degrees (horizontal in Fig 2.7). The normal stress on that plane is equal to σ1, so the plane is represented by the point on the circle where σn = σ1. Next, consider a vertical plane, so perpendicular to σ3, meaning that σn = σ3; the point representing the plane plots along on the circle at that location. The arc between both points is 180 degrees, representing the double angle 2θ. When we understand its construction, the Mohr diagram is complete and we can read off the value of σn,P along the σn-axis, and the value of σs,P along the σs-axis for our plane P, as shown in Figure 2.9. (Note that alternative conventions for this construction are also used, so be careful that they are not mixed.)

We see that:

σn,P = 1⁄2(σ1 + σ3) + 1⁄2(σ1 – σ3) cos 2θ

and

σs,P = 1⁄2(σ1 – σ3) sin 2θ

FIGURE 2.9. For each value of the shear stress and the normal stress there are two corresponding planes, as shown in the Mohr diagram (a). The corresponding planes in σ1 – σ3 space are shown in (b).

A couple of additional observations can be made from the Mohr diagram (Figure 2.9). There are two planes, oriented at angle θ and its complement (90o – θ), with equal shear stresses but different normal stresses. Also, there are two planes with equal normal stress, but with shear stresses of opposite sign (that is, they act in different directions on these planes).

In general, for each orientation of a plane, defined by its angle θ, there is a corresponding point on the circle. The coordinates of that point represent the normal and shear stresses that act on that plane. For example, when θ = 0° (that is, for a plane parallel to σ3), P coincides with σ1, which gives σn = σ1 and σs = 0. In other words, for any value of σ1 and σ3 (σ3 = σ2 in our compression experiment), we can determine σn and σs graphically for planes that lie at an angle θ with σ3. If we decide to change our earlier experiment by gluing the planks to the clay block and then moving the planks apart (a tension experiment), we must use a negative sign for the least principal stress (in this case, σ1 = σ2 and σ3 is negative). So the center O of the Mohr circle can lie on either side of the origin, but is always on the σ-axis.

The Mohr diagram also nicely illustrates the attitude of planes along which the shear stress is greatest for a given state of stress. The point on the circle for which σs is maximum corresponds to a value of 2θ = 90°. For the same point, the magnitude of σs is equal to the radius of the circle, that is, 1⁄2(σ1 – σ3). Thus the (σ1 – σ3), the differential stress, is twice the magnitude of the maximum shear stress:

σd = 2σs,max Eq. 2.16

When there are changes in the principal stress magnitudes without a change in the differential stress, the Mohr circle moves along the σn-axis without changing the magnitude of σs. In our experiment, this would be achieved by increasing the air pressure in the classroom or carrying out the experiment under water, both of which can be uncomfortable; this “surrounding” pressure is called the confining pressure (Pc) of the experiment. In Chapter 3 we return to the Mohr stress diagram and the role of the confining pressure for fracturing of rocks, but let’s get comfortable with the construction with a simple assignment that is in the Supplements section.

2.6 STRESS STATES

If the three principal stresses are equal in magnitude, we call the stress isotropic. This stress state is represented by a sphere rather than an ellipsoid, because all three radii are equal. If the principal stresses are unequal in magnitude, the stress is called anisotropic. By convention, the maximum principal stress is given the symbol σ1, the intermediate and minimum principal stresses acting along the other two axes are given the symbols σ2 and σ3, respectively. Thus, by (geologic) convention σ1 ≥ σ2 ≥ σ3.

By changing the relative values of the three principal stresses we define several common stress states:

General triaxial stress: σ1 > σ2 > σ3 ≠ 0
Biaxial (plane) stress: one axis = 0 (e.g., σ1 > 0 > σ3)
Uniaxial compression: σ1 > 0; σ2 = σ3 = 0
Uniaxial tension: σ1 = σ2 = 0; σ3 < 0
Pressure (Hydrostatic/Lithostatic stress): σ1 = σ2 = σ3

So, we learned that the stress state of a body is defined by nine components. Mathematically this ellipsoid is described by a 3 × 3 matrix (called a second-rank tensor). For the purposes of our examination it is sufficient to use a mostly geometric approach of stress, as we do here, but for a fuller analysis of stress in bodies it is useful to apply mathematical operations and transformations, which involve tensor algebra (see Supplementary Materials).

Common Stress States in Mohr Space

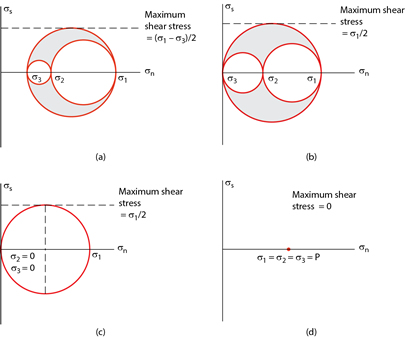
Let’s look at the representation of various stress states with the Mohr construction, which further highlights the power of this method, as it resolves stress in 3D that would otherwise require cumbersome trigonometric calculations (much longer than the 2D derivations above). The three-dimensional Mohr diagrams in Figure 2.10 may at first appear a lot more complex than those in our earlier examples, because they represent three-dimensional stress states rather than two-dimensional conditions. Three-dimensional Mohr constructions simply combine three two-dimensional Mohr circles for (σ1 – σ2), (σ1 – σ3), and (σ2 – σ3), and each of these three Mohr circles adheres to the procedures outlined earlier.

FIGURE 2.10. Mohr diagrams of some representative stress states: (a) triaxial stress, (b) biaxial (plane) stress, (c) uniaxial compression, and (d) isotropic stress or hydrostatic pressure, P (compression is shown).

Figure 2.10a shows the case for general triaxial stress, in which all three principal stresses have nonzero values (σ1 > σ2 > σ3 ≠ 0). Biaxial (plane) stress, in which one of the principal stresses is zero (e.g., σ3 = 0) is shown in Figure 2.10b. Uniaxial compression (σ2 = σ3 = 0; σ1 > 0) is shown in Figure 2.10c, whereas uniaxial tension (σ1 = σ2 = 0; σ3 < 0) would place the Mohr circle on the other side of the σn-axis. Finally, isotropic stress, often called hydrostatic pressure, is represented by a single point on the σn-axis of the Mohr diagram (positive for compression, negative for tension), because all three principal stresses are equal in magnitude (σ1 = σ2 = σ3; Figure 2.10d).

2.7 ISOTROPIC STRESS AND NON-ISOTROPIC STRESS

In later chapters we’ll see how stresses result in rock deformation, and how stress and strain are related. Given of a body’s response to stress states, we subdivide stress into two components, the isotropic or mean stress and the non-isotropic stress (Figure 2.11). The mean stress is defined as (σ1 + σ2 + σ3)/3, using the symbol σ3. Note that the mean stress is typically greater than σ3 (so, (σ3 - σm) < 0) and smaller than σ1 (so, (σ1 - σm) > 0). The difference between mean stress and total stress is the deviatoric stress (σdev), so:

σ = σm + σdev Eq. 2.17

FIGURE 2.11. The isotropic (mean) and non-isotropic (deviatoric) components of stress. (a) Isotropic, mean stress causes volume change and (b) non-isotropic, deviatoric stress causes shape change.

The mean stress is often called the hydrostatic component of stress or the hydrostatic pressure, because a fluid is stressed equally in all directions. Because the magnitude of the hydrostatic stress is equal in all directions it is an isotropic stress component. When we consider rocks at depth in the Earth we generally refer to lithostatic (or overburden) pressure, Pl, rather than the hydrostatic pressure. The lithostatic stress component is best explained by a simple but powerful calculation. Consider a rock at a depth of 3 km in the middle of a continent. The lithostatic pressure at this point is a function of the weight of the overlying rock column because other (tectonic) stresses are unimportant. The local pressure is a function of rock density, depth, and gravity:

Pl = ρ ⋅ g ⋅ h Eq. 2.18

If ρ (density) equals a representative crustal value of 2,700 kg/m3, g (gravity) is 9.8 m/s2, and h (depth) is 3,000 m, we get:

Pl = 2,700 ⋅ 9.8 ⋅ 3,000 = 79.4 ⋅ 106 Pa ≈ 80 MPa (or 800 bars)

In other words, for every kilometer in the Earth’s crust the lithostatic pressure increases by approximately 27 MPa. With depth the density of rocks increases, so you cannot continue to use the value of 2,700 kg/m3. For crustal depths greater than approximately 15 km the average density of the crust is 2,900 kg/m3. Deeper into Earth the density increases further, reaching as much as 13,000 kg/m3 in the solid inner core.

Because the lithostatic pressure is of equal magnitude in all directions, it follows that σ1 = σ2 = σ3. The actual state of stress on a body at depth in the Earth is often more complex than only that from the overlying rock column. Anisotropic stresses that arise from tectonic processes, such as the collision of continental plates or the drag of the plate on the underlying material, contribute to the stress state at depth. The differential stresses of these anisotropic stress components, however, are many orders of magnitude less than the lithostatic stress. In the crust, differential stresses may reach a few hundred megapascals, but in the mantle, where lithostatic pressure is high, they are only on the order of tens of megapascals or less (see below). Yet, such low differential stresses are responsible for the slow motion of “solid” mantle that is a critical element of our planet’s plate dynamics.

Let’s return to Figure 2.11 and the preceding comments. Why divide a body’s stress state into an isotropic (lithostatic/hydrostatic) and an anisotropic (deviatoric) component? For our explanation we return to look at the deformation of a stressed body. Because isotropic stress acts equally in all directions, it results in a volume change of the body (Figure 2.11a). Isotropic stress is responsible for the consequences of increasing water pressure at depth on a human body or air pressure changes during take-off and landing of a plane (remember those painfully popping ears?). Place an air-filled balloon under water and you will see that isotropic stress maintains the spherical shape of the balloon, but reduces the volume. Deviatoric stress, on the other hand, changes the shape of a body (Figure 2.11b). As we will see in Chapter x, distortion of a body can often be measured in structural geology, but volume change is considerably more difficult to determine. As in determining distortions, knowledge about the original volume of a body is the obvious way to determine any volume change. Reliable volume markers, however, are rare in rocks and we resort to indirect approaches such as chemical contrasts between deformed and undeformed samples. The division between the isotropic and anisotropic components of stress provides the connection between the volumetric and distortional components of deformation, respectively.

2.8 METHODS OF STRESS MEASUREMENT

Up to this point our discussion of stress has been pretty theoretical, except perhaps for our classroom experiment with clay and the example of kicking a ball around. Before you forget that stress is a physical quantity rather than an abstract concept (as in psychology), we will close this chapter with a few notes on stress measurements and an application. Because the methods of present-day stress measurements are explained in most engineering texts on rock mechanics, the more common methods are briefly summarized here:

Borehole breakouts - The shape of a borehole changes after drilling in response to stresses in the host rock. Specifically, the hole becomes elliptical with the long axis of the ellipse parallel to minimum horizontal stress (σmin, hor).
Hydrofracture - If water is pumped under sufficient pressure into a well that is sealed off, the host rock will fracture. These fractures will be parallel to the maximum principal stress (σ1), because the water pressure necessary to open the fractures is equal to the minimum principal stress.
Strain release - A strain gauge, consisting of tiny electrical resistors in a thin plastic sheet, is glued to the bottom of a borehole. The hole is drilled deeper with a hollow drill bit (called overcoring), thereby separating the core to which the strain gauge is connected from the wall of the hole. The inner core expands (by elastic relaxation), which is measured by the strain gauge. The direction of maximum elongation is parallel to the direction of maximum compressive stress and its magnitude is proportional to stress according to Hooke’s Law (elasticity).
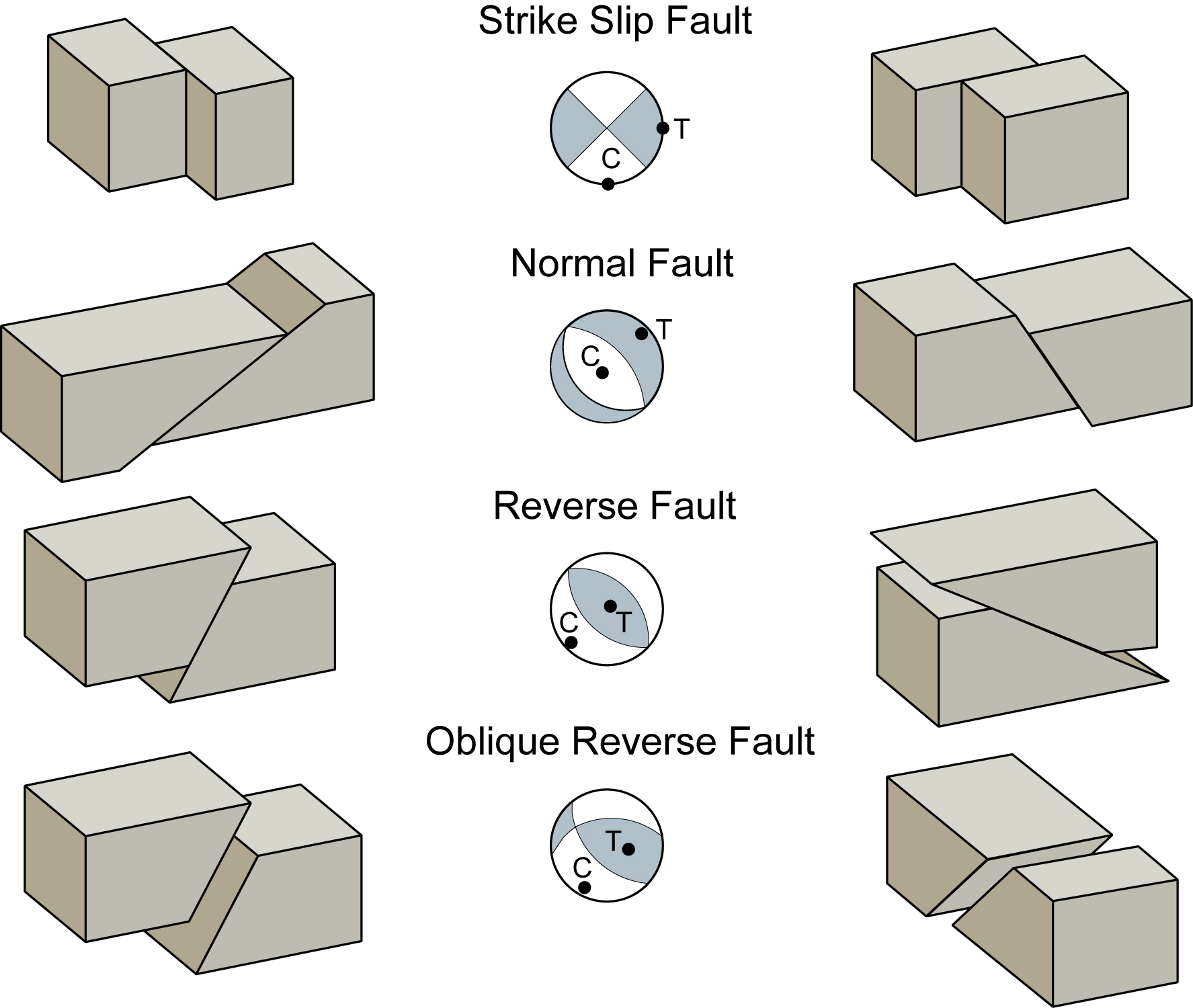
Fault-plane solutions - When an earthquake occurs, records of the first motion on seismographs around the world divide the world into two sectors of compression and two sectors of tension. These zones are separated by the orientation of two perpendicular planes. One of these planes is the fault plane on which the earthquake occurred, and from the distribution of compressive and tensile sectors, the sense of slip on the fault can be determined. We assume that the bisector of the two planes in the tensile field (T) represents the minimum principal stress (σ3) and the bisector in the compressive field (C), parallel to the maximum compressive stress (σ1); Figure 2.12. You can learn more about focal mechanisms in this 6min narrated animation (IRIS).

Figure 2.12. Fault types and fault-plane solutions (or focal mechanism solutions). First-motion earthquake analysis identifies areas of Tension (T, blue) and Compression (C, white) that and define fields in stereographic projection, separated by two planes, with one of these the active fault. These “beachballs” have characteristic patterns for strike slip, normal and reverse faults, and combinations. Today’s global earthquake network instantaneously produces these patterns for analysis. (from USGS)

2.8.1 Present-Day Stress

As it turns out, it is quite difficult to obtain a reliable measure of present-day stress in the Earth. The determination of the absolute magnitude of the stress is particularly challenging. Generally, stress determinations give the stress differences (the differential stress) and the orientation of the principal stresses, using earthquake focal mechanisms, well-bore enlargements (or “breakouts”), and other in situ stress measurements, and the analysis of faults and fractures. Earthquake focal mechanisms define a set of two possible fault planes and slip vectors, which are assumed to parallel the maximum resolved shear stress on these planes. Several focal mechanisms and slip vectors on faults of different orientation are used to determine the (best-fit) principal stress axes. The magnitude of stress is based on the energy release of earthquakes, but this relationship is incomplete. The analysis of the orientation of exposed faults and their observed slip uses a similar inversion approach. The elliptical distortion of vertical wells that were drilled for petroleum and gas exploration is a direct gauge of the local stress field and is widely available; the long axis of the distortion is parallel to the horizontal, minimum principal stress. Other in situ stress measurements, such as hydraulic fracturing, in which a hole is capped and pressurized by a fluid until fracturing releases the fluid pressure, reflect the local stress field. Whether this local field reflects the regional (or, remote) tectonic stress or merely the conditions surrounding the particular geo logic feature, including the role of pore pressure, is a topic of ongoing debate.

We can get an intuitive sense of differential stress magnitudes in nature from a simple consideration of mountainous regions. We have all looked in awe at steep walls of rock, especially when they are scaled by climbers. In the western Himalayas, vertical cliffs rise up to 2,000 m above the valleys. Using Equation 2.18, we can calculate the vertical stress at the base of such cliffs is >50 MPa (2,700 kg/m3 × 9.8 m/s2 × 2,000 m = 53 MPa), while the minimum horizontal stress (that is, atmospheric pressure) is only about 0.1 MPa. Of course mountain ranges of 6–9 km high are not vertical cliffs, so we require a modification of Equation 2.18 to get the differential stress from the load of mountains. Using a triangular mountain load with height h, we get (without showing the derivation):

σd ≈ 0.5 ρ ⋅ g ⋅ h Eq. 2.19

Present-day stress determinations, like borehole measurements, give differential stress magnitudes that range from tens to hundreds of megapascals, which are slightly less than the lithospheric load (Pl). Realize, though, that these methods can only record stress magnitudes in the outermost part (upper crust) of Earth, such as deep borehole measurements from Germany’s KTB shown in Figure 2.13. The magnitude of differential stresses deep in Earth is understood when we learn about Earth’s thermal structure and deformation mechanisms of plastic deformation, where differential stresses are one to two orders of magnitude smaller, and much less than lithospheric pressure.

Figure 2.13. In situ borehole measurements of differential stress (σd) with depth (and with approximate temperature) at the KTB borehole in the Bohemian Massif (southern Germany), which ended at a depth of 9101 m.

Note that the best fit line of differential stress with depth (red) changes at the frictional-plastic transition (gray dashed line), which we’ll examine in later chapters.

2.8.2 Global Stress Patterns

From large data sets of present-day stress measurements we find that the results are generally in good agreement about the orientation of the principal stresses and that they compare reasonably well in magnitude. An application of these approaches and the information that they provide about regional stress patterns and plate dynamics is shown in Figure 2.14. This global synthesis of stress data, part of the World Stress Map project, reflects an international effort that catalogs present-day stress patterns around the world. The majority of stress determinations are from earthquake focal mechanism solutions.

FIGURE 2.14. The World Stress map displays over 11,000 data records of the WSM 2008 release. Red indicates Normal Faulting (NF), green indicates Strike-Slip (SS), blue indicates Thrust Faulting (TF) and "U" is an unknown tectonic regime. The black lines are the major plate boundaries. Link: high-res version. (http://dc-app3-14.gfz-potsdam.de/pub/stress_data/stress_data_frame.html)

The global stress map illustrates regionally systematic stress fields in the upper crust, despite the geologic complexity found at Earth’s surface. The orientation and magnitudes of horizontal principal stresses are uniform over areas hundreds to thousands of kilometers in extent. These data also show that the upper crust is generally under compression, meaning that maximum compressive stresses are horizontal, resulting in either reverse or strike-slip faulting. For example, the maximum stress in the eastern half of North America is oriented approximately NE–SW with differential stresses on the order of a hundred megapascals. Areas where horizontal tensile stresses dominate are regions of active extension, such as the East African Rift zone, the Basin and Range of western North America, and high plateaus in Tibet and western South America. Using this compilation we can divide the global stress field into stress provinces, which generally correspond to active geologic provinces. From this, a pattern emerges that is remarkably consistent with the broad predictions from the main driving forces of plate tectonics (such as the pull of the downgoing slab in subduction zones and “push” at ocean ridges) and with the effects of plate interactions (such as continent–continent collision). In a later chapter we’ll revisit the driving forces of plate tectonics. When studying these global patterns you must realize that they only reflect the present-day stress field. Many of the world’s geologic provinces reflect ancient tectonic activity, with configurations and processes that are no longer active today, and the present-day global stress pattern is unrelated to this past activity. For example, the orientation of today’s compressive stresses in eastern North America reflect the opening of the Atlantic Ocean. They are at a high angle to late Paleozoic compressive stresses, which resulted from compressional Appalachian-Caledonian activity at the margin.

What happens at depth? While lithostatic pressure increases with depth (see Equation 2.18), differential stress cannot increase without bounds, because the rocks that comprise the Earth do not have infinite strength. Strength is the ability of a material to support differential stress; in other words, it is the maximum stress before rocks fail by fracturing or flow. Combining present-day stress and paleostress data with experimental data on flow properties of rocks and minerals gives generalized strength profiles for Earth. These strength curves (Figure 2.15) represent the differential stress magnitude with depth, given assumptions on the composition and temperature of rocks. At this point we include representative strength curves without much explanation just to give you an idea of stress magnitudes with depth, distinguishing between old (low geothermal gradient) and young (high geothermal gradient) areas, representing Precambrian cratons and Mesozoic/Cenozoic collisional belts, respectively.

FIGURE 2.15. Strength curves showing the variation in differential stress magnitude with depth in Earth for (a) a region characterized by a low geothermal gradient (e.g., Precambrian shield areas) and (b) a region with a high geothermal gradient (e.g., areas of continental extension).

Differential stresses are largely based on experimental data for brittle failure and ductile flow, which change as a function of composition and temperature. In these diagrams the only compositional change occurs at the crust-mantle boundary (the Moho); in the case of additional compositional stratification, more drops and rises will be present in the strength curve. The vertical bars (red) at the right of each diagram indicates where seismic activity may occur.

You remember from your introductory geology class that the outermost rheologic layer of the Earth is called the lithosphere, comprising the crust and part of the upper mantle, which overlies the asthenosphere. Taking a quartzo-feldspathic crust and an olivine-rich upper mantle, a low geothermal gradient (about 10°C/km), and a crustal thickness of about 40 km, produces the lithospheric strength curve in Figure 2.15a. You will notice that a sharp decrease in strength occurs around 25 km, which reflects the change from brittle to plastic flow (called the frictional–plastic transition) in quartzo-feldspathic rocks. The properties of an olivine-rich mantle are quite different from the crust, and this in turn produces a sharp increase in strength and, therefore, a return to brittle behavior at the crust-mantle boundary (the Moho). As with the crustal profile, strength decreases as plastic behavior replaces the brittle regime of mantle rocks with depth. This frictional versus plastic behavior of rock is strongly dependent on temperature, as demonstrated by creating a strength profile at a higher geothermal gradient (Figure 2.15b), which promotes plastic flow and reduces the strength up to one order of magnitude. With a geothermal gradient of 20°C/km, the frictional–plastic transition now occurs at a depth of about 10 km. In all cases the deeper mantle is mechanically weak, because it is characterized by high temperatures, meaning that the mantle only supports differential stresses on the order of a few megapascals. When considering strength profiles, remember the distinction between differential stress and lithostatic pressure. The lithostatic pressure always becomes greater with depth in the Earth, and is orders of magnitude greater than the differential stress. For example, the lithostatic stress at a depth of 100 km in the Earth is several thousand megapascals (use Equation 2.16), but the differential stress is only on the order of 1–10 MPa!

2.8.3 Paleostress

If we wish to compare modern stress values with ancient stresses from rocks, most of the approaches listed above are not suitable. For the analysis of paleostress we are essentially limited to the analysis of fault and fracture data, and to microstructural approaches such as grain-size determinations and grain deformation analysis. Fault-slip analysis requires some understanding of fault mechanics (Chapter 3), but, in short, it uses fault orientation and the sense of slip on that fault with the assumption that the slip direction parallels the maximum shear stress in that plane. Numerical analysis of sufficiently large fault data sets can provide the reduced stress tensor that contains the orientations of the three principal stresses and the differential stress ratio, (σ2 – σ3)/(σ1 – σ2), which ranges from 0 (when σ2 = σ3) to 1 (when σ1 = σ2).

Stress from microstructural methods requires an understanding of crystal plastic processes and the development of microstructures, which are discussed later, in the Plastic Regime chapters. The grain size of plastically deformed rocks that involves dislocation creep (Chapter 7), is (non-linearly) related to the differential stress magnitude, based on laboratory experiments at representative pressure and temperature conditions. Similarly, the development of deformation microstructures of individual grains, like crystal twins, is a function of the differential stress. Collectively, these approaches can constrain the differential stress magnitudes at many depths in Earth, complementing upper crustal data from fault studies and present-day stress determinations. Whereas the latter methods remain unexplained at this point, some of the information that is obtained from them was incorporated in the section on Earth’s global stress.

Back to Force&Stress Contents

Back to PSG&T Home

v3.0; last update 14-sep-23

[1] After English physicist Isaac Newton (1642–1727).

[2] German-born theoretical physicist (1879–1955).

[3] After French mathematician Blaise Pascal (1623–1662).

[4] Named after German engineer Otto Mohr (1835–1918).