3. The Frictional Regime
Drop a glass on a tile floor and watch as it breaks into dozens of pieces; you have just witnessed an example of brittle deformation! Because you’ve probably broken a glass or two (or a plate or a vase) and have seen cracked buildings, sidewalks, or roads, you already have an intuitive feel for what brittle deformation is all about. In the upper crust of the Earth, roughly 10 km in depth, rocks undergo deformation in the frictional regime, creating a myriad of brittle structures and associated features. Why study frictional behavior and brittle deformation? For starters, since rocks deform in a brittle manner under the range of pressures and temperatures found at or near the Earth’s surface (down to 10–15 km), fractures pervade rocks of the upper crust. In fact every rock outcrop that you will ever see contains fractures at some scale. Because they are so widespread, faults and fractures play a major role in determining the permeability and strength of rock, and the resistance of rock to erosion. They also affect the velocity and direction of toxic waste transport, the location of an ore deposit, the durability of a foundation, the stability of a slope and landslides, the suitability of a reservoir, the safety of a mine shaft, the form of a landscape, and so on. Lastly, frictional behavior is the underlying cause of earthquakes, and, on a large scale, contributes to the evolution of regional tectonics. In this chapter we introduce the basic terminology and concepts of deformation in the frictional regime, explain the processes by which it takes place, and examine the physical conditions.
|
|
|
FIGURE 3.1. A geologist measuring fractures in an outcrop, near Tuross Point (southeastern Australia). The more intensely fractured rock is a fine-grained mafic intrusive and the less fractured rock is a coarse-grained felsic intrusive. [6.1] |
Brittle Deformation
Research in the last few decades has changed the way geologists think about brittle deformation and, as a consequence, the vocabulary of brittle deformation has evolved. We discuss the key terminology and processes in this chapter while Supplementary Materials includes additional definitions of terms that you may come across when reading articles on this topic. Remember that some of this vocabulary is controversial, and you will find that not all geologists agree on the definitions that we provide. In fact, may geologists use brittle regime as a synonym to frictional regime. Instead, we intentionally distinguish between brittle deformation for descriptive elements and the processes that define deformation in the frictional regime. We will return to the possibly confusing use of this terminology after the introduction of plastic processes and strain in Chapter 7.
Brittle deformation is the permanent change that occurs in a solid material due to the growth of fractures and/or due to sliding on fractures once they have formed. In this definition, a fracture is any surface of discontinuity, meaning a surface across which the material is no longer bonded (Figure 3.1). If a fracture fills with minerals precipitated out of a hydrous solution, it is a vein, and if it fills with (igneous or sedimentary) rock originating from else- where, it is a dike. A joint is a natural fracture in rock across which there is no measurable shear displacement. Because of the lack of shear involved in joint formation, joints can also be called cracks or tensile fractures. Shear fractures, in contrast, are mesoscopic fractures across which there has been displacement. Sometimes geologists use the term “shear fracture” instead of “fault” when they wish to imply that the amount of shear displacement on the fracture is relatively small, and that the shear displacement accompanied the formation of the fracture in once intact rock. In Chapter 4 we will show several examples of fractures and veins in natural rocks and examine their history.
In a broad sense, a fault is a surface or zone on which there has been measurable displacement. In a narrower sense, geologists restrict use of the term fault to a fracture surface on which there has been sliding. When using this narrow definition of fault, we apply the term fault zone to refer either to a band of finite width across which the displacement is partitioned among many smaller faults, or to the zone of rock bordering the fault that has fractured during faulting. Chapter 5 examines examples and settings of natural faults. Here, we apply the term shear zone to a band of finite width in which the shear strain is significantly greater than that in the surrounding rock. Movement in shear zones can be the consequence of cataclasis (distributed fracturing, crushing, and frictional sliding of grains of rock or rock fragments), crystal-plastic deformation mechanisms (dislocation glide, dislocation climb), and diffusion. Given that strain is distributed in such zones, the term ductile shear zone is often used. We’ll examine cataclastic shear zones in this chapter, but other types of ductile deformation is be discussed in later chapters.
Categories of Brittle Deformation
For purposes of our discussion, we divide brittle deformation processes into four categories that are listed below and illustrated in Figure 3.2.
- Tensile cracking. This type of brittle deformation involves propagation of cracks into previously unfractured material when a rock is subjected to a tensile stress (Figure 3.2b). If the stress field is homogeneous, tensile cracks propagate in their own plane and are perpendicular to the least principal stress (σ3).
- Shear rupture. This type of brittle deformation results in the initiation of a macroscopic shear fracture at an acute angle to the maximum principal stress when a rock is subjected to a triaxial compressive stress (Figure 3.2c). Shear rupturing involves growth and linkage of microcracks.
- Frictional sliding. This process refers to the occurrence of sliding on a preexisting fracture surface, without the significant involvement of plastic deformation mechanisms (Figure 3.2d and f).
- Cataclastic flow. This type of brittle deformation refers to macroscopic ductile (=distributed) flow as a result of grain-scale fracturing and frictional sliding distributed over a band of some width (Figure 3.2e and g).
|
|
|
FIGURE 3.2. Types of brittle deformation. (a) Orientation of the remote principal stress directions with respect to an intact rock body. (b) A tensile crack, forming parallel to σ1 and perpendicular to σ3 (which may be tensile). (c) A shear fracture, forming at an angle of about 30° to the σ1 direction. (d) A tensile crack that has been reoriented with respect to the remote stresses and becomes a fault by undergoing frictional sliding. (e) A tensile crack which has been reactivated as a cataclastic shear zone. (f) A shear fracture that has evolved into a fault. (g) A shear fracture that has evolved into a cataclastic shear zone. [6.4] |
PROCESSES OF BRITTLE DEFORMATION
A brittle fault is a surface on which measurable slip has developed without much contribution by plastic deformation mechanisms. Brittle faulting happens in response to the application of a differential stress, because slip occurs in response to a shear stress parallel to the fault plane. In other words, for faulting to take place, σ1 cannot equal σ3, and the fault surface cannot parallel a principal plane of stress. Faulting causes a change in shape of the overall rock body that contains the fault. Hence, faulting contributes to development of regional strain; however, because a brittle fault is, by definition, a discontinuity in a rock body, the occurrence of faulting does not require development of measurable ductile strain in the surrounding rock.
There are two basic ways to create a brittle fault (Figure 3.2). The first is by shear rupturing of a previously intact body of rock. The second is by shear reactivation of a previously formed weak surface (for example, a joint, a bedding surface, or a preexisting fault) in a body of rock. A preexisting weak surface may slip before the differential stress magnitude reaches the failure strength for shear rupture of intact rock. Once formed, movement on brittle faults takes place either by frictional sliding, by the growth of fault-parallel veins, or by cataclastic flow. We’ll focus mostly on fault formation and friction, the central processes of brittle faulting, and only briefly mention the other processes here.
An Atomistic View
To understand brittle deformation we need to look at the atomic structure of materials. Solids are composed of atoms or ions that are connected to one another by chemical bonds that can be thought of as tiny springs. Each chemical bond has an equilibrium length, and the angle between any two chemical bonds connected to the same atom has an equilibrium value (Figure 3.3a). During elastic strain, the bonds holding the atoms together within the solid stretch, shorten, and/or bend, but they do not break (Figure 3.3)! When the stress is removed, the bonds return to their equilibrium conditions and the elastic strain disappears. In other words, elastic strain is fully recoverable. This elastic property of solids explains the propagation of earthquake waves through Earth.
Rocks cannot accumulate large elastic strains; you certainly cannot stretch a rock to twice its original length and expect it to spring back to its original shape! At most, a rock can develop a few percent strain by elastic distortion. If the stress applied to a rock is greater than the stress that the rock can accommodate elastically, then one of two changes can occur: the rock deforms in a ductile manner (strain without breaking), or the rock deforms in a brittle manner (that is, it breaks).
What actually happens during brittle deformation? Basically, if the stress becomes large enough to stretch or bend chemical bonds so much that the atoms are too far apart to attract one another, then the bonds break, resulting in either formation of a fracture (Figure 3.3c) or slip on a preexisting fracture. In contrast to elastic strain, brittle deformation is non-recoverable, meaning that distortion remains when the stress is removed. Again we use earthquake rupture as an example; in this case, elastic strain is exceeded at the focus, resulting in failure and displacement. The pattern of breakage during brittle deformation depends on stress conditions and on material properties of the rock, so brittle deformation does not involve just one process.
|
|
|
FIGURE 3.3. A sketch illustrating what is meant by stretching and breaking of atomic bonds. The chemical bonds are represented by springs and the atoms by spheres. (a) Four atoms arranged in a lattice at equilibrium. (b) As a consequence of stretching of the lattice, some bonds stretch and some shorten, and the angle between pairs of bonds changes. (c) If the bonds are stretched too far, they break, and elastic strain is released. [6.3] |
TENSILE CRACKING
In Figure 3.4 we illustrate a crack in rock on the atomic scale. One way to create such a crack would be for all the chemical bonds across the crack surface to break at once. In this case, the tensile stress necessary for this to occur is equal to the strength of each chemical bond multiplied by all the bonds that had once crossed the area of the crack. If you know the strength of a single chemical bond, then you can calculate the stress necessary to break all the bonds simply by multiplying the bond strength by the number of bonds. However, in order to better understand tensile cracking behavior of materials, we first introduce a fundamental rheological concept, elasticity.
|
|
FIGURE 3.4. A cross-sectional sketch of a crystal lattice (balls are atoms and sticks are bonds) in which there is a crack. The crack is a plane of finite extent across which all atomic bonds are broken. [6.5] |
Elasticity
What is elastic behavior and how is it relevant for deformed rocks? Let’s first look at relevance. In the field of seismology, the study of earthquakes, elastic properties are very important. As you know, seismic waves from an earthquake pass through the Earth to seismic monitoring stations around the world. As they travel, these seismic waves briefly deform the rocks, but after they have passed, the rocks return to their undeformed state. To imagine how rocks are able to do so we turn to a common analog: a rubber band. When you pull a rubber band, it extends; when you remove this stress, the band returns to its original shape. The greater the stress, the farther you extend the band. Beyond a certain point, called the failure stress, the rubber band breaks and brings a painful end to the experiment. This ability of rubber to extend lies in its atomic structure. The bond lengths between atoms and the angles between bonds in a crystal structure represent a state of lowest potential energy for a crystal. These bonds are able to elongate and change their relative angles to some extent, without introducing permanent changes in the crystal structure. Rubber bands extend particularly well because rubber can accommodate large changes in the angular relationships between bonds; however, this causes a considerable increase in the potential energy, which is recovered when we let go of the band, or when it snaps. So, once the stress is released, the atomic structure returns to its energetically most stable configuration, that is, the lowest potential energy. Like the elasticity of a rubber band, the ability of rocks to deform elastically also resides in nonpermanent distortions of the crystal lattice, but unlike rubber, the magnitude of this behavior is relatively small in rocks.
Expressing elastic behavior in terms of stress and strain, we get:
σ = E ⋅ e Eq. 3.1
where E is a constant of proportionality called Young’s modulus (also called stiffness) that describes the slope of the line in the σ–e diagram (tangent of angle θ; Figure 3.5). The unit of this elastic constant is Pascal (Pa = kg/m ⋅ s–2), which is the same as that of stress (recall that strain is a dimensionless quantity). Typical values of E for crustal rocks are on the order of –1011 Pa [Note: we require a negative sign to produce a negative elongation (shortening) from applying a compressive (positive) stress]. Linear Equation 5.3 is also known as Hooke’s Law[1], which describes elastic behavior; we use a spring as the physical model for this behavior. Young’s moduli for representative materials are below, showing that rock is orders of magnitude stiffer than a rubber band:
|
Material |
E (GPa) |
|
Rubber |
0.05 |
|
Iron (Fe) |
196 |
|
Quartz |
72 |
|
Salt |
40 |
|
Sandstone |
10-20 |
|
Shale |
5-70 |
|
Limestone |
80 |
|
Marble |
50-70 |
|
Granite |
50 |
|
Gabbro |
50-100 |
|
|
|
FIGURE 3.5. Models of linear rheologies. Physical model consisting of a spring, and associated strain–time and stress–strain curves for (a) elastic behavior. Symbols used: e = elongation, σ = stress, E = elasticity, t = time, el denotes elastic strain component. |
We can similarly describe elastic behavior in terms of the shear stress, σs:
σs = G ⋅ γ Eq. 3.2
where G is another constant of proportionality, called the shear modulus or the rigidity, and γ is the shear strain. The corresponding constant of proportionality in volume change (dilation) is called the bulk modulus, K:
σ = K ⋅ [(V – Vo)/Vo] Eq. 3.3
Perhaps an easier way to understand the bulk modulus is using its inverse, 1/K, which is the compressibility of a material. Some representative values for bulk and shear moduli are:
|
Crystal |
K |
G |
|
Iron (Fe) |
1.7 |
0.8 |
|
Copper (Cu) |
1.33 |
0.5 |
|
Silicon (Si) |
0.98 |
0.7 |
|
Halite (NaCl) |
0.14 |
0.26 |
|
Calcite (CaCO3) |
0.69 |
0.37 |
|
Quartz (SiO2) |
0.3 |
0.47 |
|
Olivine (Mg2SiO4) |
1.29 |
0.81 |
|
Ice (H2O) |
0.073 |
0.025 |
|
In 1011 Pa at atmospheric pressure and room temperature. |
||
It is also quite common to use an alternative to the bulk modulus that expresses the relationship between volume change and stress, called Poisson’s ratio[2], represented by the symbol ν. This elastic constant is defined as the ratio of the elongation perpendicular to the compressive stress and the elongation parallel to the compressive stress:
ν = eperpendicular/eparallel Eq. 3.4
Poisson’s ratio describes the ability of a material to shorten parallel to the compression direction without corresponding thickening in a perpendicular direction. Therefore the ratio ranges from 0 to 0.5, for fully compressible to fully incompressible materials, respectively. Incompressible materials maintain constant volume irrespective of the stress. A sponge has a very low Poisson’s ratio, while a metal cylinder has a relatively high value. A low Poisson’s ratio also implies that a lot of potential energy is stored when a material is compressed; indeed, if we remove the stress from a sponge it will jump right back to its original shape. Values for Poisson’s ratio in natural rocks typically lie in the range 0.25–0.35:
|
Rock |
Poisson’s Ratio (ν) |
|
Basalt |
0.25 |
|
Gabbro |
0.33 |
|
Gneiss |
0.27 |
|
Granite |
0.25 |
|
Limestone |
0.32 |
|
Peridotite |
0.27 |
|
Quartzite |
0.10 |
|
Sandstone |
0.26 |
|
Schist |
0.31 |
|
Shale |
0.26 |
|
Slate |
0.30 |
|
Glass |
0.24 |
|
Sponge |
<<0.10 |
A central characteristic of elastic behavior is its reversibility: once you remove the stress, the material returns to its original shape. Reversibility implies that the energy introduced remains available for returning the system to its original state. This energy, which is a form of potential energy, is called the internal strain energy. Because the material is undistorted after the stress is removed, we therefore say that strain is recoverable. Thus, elastic behavior is characterized by recoverable strain. A second characteristic of elastic behavior is the instantaneous response to stress: finite strain is achieved immediately. Releasing the stress results in an instantaneous return to a state of no strain (Figure 5.3a). Both these elastic properties, recoverable and instantaneous strain, are visible in our rubber band or sponge experiments. Note that elastic behavior is complicated by the granular structure of natural rocks, where grain boundaries give rise to perturbations from perfect elastic behavior in non-granular solids like glass. A summary of elastic constants:
|
Bulk modulus (K) |
Ratio of pressure and volume change. |
|
Compressibility (1/K) |
The inverse of the bulk modulus. |
|
Poisson’s ratio (ν) |
Measure of compressibility of a material. It is defined as the ratio between elongation perpendicular to compressive stress and elongation parallel to compressive stress. |
|
Rigidity (G) |
Shear modulus. |
|
Shear modulus (G) |
Ratio of the shear stress and the shear strain. |
|
Young’s modulus (E) |
Ratio of compressive stress and longitudinal strain. |
Stress Concentration
Using realistic values for the elasticity (Young’s modulus, E) and small strain (<10%), Equation 3.1 results in a theoretical strength of rock that is thousands of megapascals. Consider granite, for example:
σ = E ⋅ e = 5⋅1010 ⋅ 0.1 = 5x103 MPa
Measurement of rock strength in the Earth’s crust shows that tensile cracking occurs at crack-normal tensile stresses on the order of 100’s to 10’s MPa, when the confining pressure is low, a value that is much smaller the theoretical strength of rock on the order of 1000’s. Keeping the concept of theoretical strength in mind, we therefore face a paradox: How can natural rocks fracture at stresses that are so much lower than their theoretical strength?
The first step toward resolving the strength paradox came when engineers studying the theory of elasticity realized that the remote stress (stress due to a load applied at a distance from a region of interest) gets concentrated at the sides of flaws (e.g., holes) inside a material. For example, in the case of a circular hole in a vertical elastic sheet subjected to tensile stress at its ends (Figure 3.6a), the local stress (i.e., stress at the point of interest) tangent to the sides of the hole is three times the remote stress magnitude (σr). The magnitude of the local tangential stress at the top and bottom of the hole equals the magnitude of the remote stress, but is opposite in sign (i.e., it is compressive). If the hole has the shape of an ellipse instead of a circle (Figure 3.6b), the amount of stress concentration, C, is equal to (2b/a) + 1, where a and b are the short and long axes of the ellipse, respectively. Thus, values for stress concentration at the ends of an elliptical hole depend on the axial ratio of the hole: the larger the axial ratio, the greater the stress concentration. For example, at the ends of an elliptical hole with an axial ratio of 8:1, stress is concentrated by a factor of 17, and in a 1 μm × 0.02 μm crack the stress is magnified by a factor of ∼100 !
|
|
FIGURE 3.6. Stress concentration adjacent to a hole in an elastic sheet. If the sheet is subjected to a remote tensile stress at its ends (σr), then stress magnitudes at the sides of the holes are equal to C.σr, where C, the stress concentration factor, is (2b/a) + 1. (a) For a circular hole, C = 3, meaning triple the stress concentration in its vicinity. (b) For an elliptical hole, C exceeds 3, further increasing the local stress concentration. [6.6]
|
With this understanding in mind, A. W. Griffith, in the 1920s, took the next step toward resolving the strength paradox when he applied the concept of stress concentration at the ends of elliptical holes to fracture development. Griffith suggested that all materials contain preexisting microcracks or flaws at which stress concentrations naturally develop, and that because of the stress concentrations that develop at the tips of these cracks, they propagate and become larger cracks even when the host rock is subjected to relatively low remote stresses. He discovered that in a material with cracks of different axial ratios, the crack with the largest axial ratio will most likely propagate first. In other words, stress at the tips of preexisting cracks can become sufficiently large to rupture the chemical bonds holding the minerals together at the tip and cause the crack to grow, even if the remote stress is relatively small. Preexisting microcracks and flaws in a rock, which include grain-scale fractures, pores, and grain boundaries, are now called Griffith cracks. Thus we resolve the strength paradox by learning that rocks in the crust are relatively weak because they contain Griffith cracks.
Griffith’s concept provided useful insight into the nature of cracking, but his theory did not adequately show how factors such as crack shape, crack length, and crack orientation affect the cracking process. In subsequent years, engineers developed a new approach to studying the problem. In this approach, called linear elastic fracture mechanics, we assume that cracks in a material have nearly infinite axial ratio (defined as long axis/short axis), meaning that all cracks are very sharp. Linear elastic fracture mechanics theory predicts that, if factors like shape and orientation are equal, a longer crack will propagate before a shorter crack. We’ll see why later in this chapter, when we discuss failure criteria. We can examine how preexisting cracks affect the magnitude of stress necessary for tensile cracking in a simple experiment. Take a sheet of paper (Figure 3.7) and pull at both ends. You have to pull quite hard in order for the paper to tear. Now make two cuts, one that is ~0.5 cm long and one that is ~2 cm long, in the edge of the sheet near its center, and pull again. The pull that you apply gets concentrated at the tip of the preexisting cuts, and at this tip the strength of the paper is exceeded. You will find that it takes much less force to tear the paper, and that it tears apart by growth of the longer preexisting cut. The reason that sharp cracks do not propagate under very small stresses is that the tips of real cracks are blunted by a crack-tip process zone, in which the material deforms plastically (Figure 3.7c).
|
|
FIGURE 3.7. Illustration of a home experiment to observe the importance of preexisting cracks in creating stress concentrations. (a) An intact piece of paper is difficult to pull apart. (b) Two cuts, a large one and a small one, are made in the paper. (c) The larger preexisting cut propagates. In the shaded area, a region called the process zone, the strength of the material is exceeded and fails. [6.7] |
It is implicit in our description of crack propagation that the total area of a crack does not form instantaneously, but rather a crack initiates at a small flaw and then grows outward. If you have ever walked out on thin ice covering a pond, you are well aware of this fact. As you move away from shore, you suddenly hear a sound like the echo of a gunshot; this is the sound of a fracture forming in the ice due to the stress applied by your weight. If you have the presence of mind under such precarious circumstances to watch how the crack forms, you will notice that the crack initiates under your boot, and propagates outwards into intact ice at a finite velocity. This means that at any instant, only chemical bonds at the crack tip are breaking. In other words, not all the bonds cut by a fracture are broken at once, and thus the basis we used for calculating theoretical strength in the first place does not represent processes under natural conditions.
AXIAL EXPERIMENTS
Let’s consider what happens during a laboratory experiment in which we stretch a rock cylinder along its axis under a relatively low confining pressure (Figure 3.8a), a process called axial stretching. As soon as the remote tensile stress is applied, preexisting microcracks in the sample open slightly, and the remote stress is magnified to create larger local stresses at the crack tips. Eventually, the stress at the tip of a crack exceeds the strength of the rock and the crack begins to grow. If the remote tensile stress stays the same after the crack begins to propagate, then the crack continues to grow, and can eventually reach the sample’s margins. When this happens, the sample fails, meaning it separates into two pieces that are no longer connected (Figure 3.8b).
|
|
FIGURE 3.8. Development of a throughgoing crack in a block under tension. (a) When tensile stress (σt) is applied, Griffith cracks open up. (b) The largest, properly oriented cracks propagate to form a throughgoing crack. [6.8]
|
We can also induce tensile fracturing by subjecting a rock cylinder to axial compression, under conditions of low confining pressure. Under such stress conditions, mesoscopic tensile fractures develop parallel to the cylinder axis (Figure 3.9a), a process known as longitudinal splitting. Longitudinal splitting is similar to tensile cracking except that, in uniaxial compression, the cracks that are not parallel to the σ1 direction are closed, whereas cracks that are parallel to the compression direction can open up. To picture this, imagine an envelope standing on its edge. If you push down on the top edge of the envelope, the sides of the envelope pull apart, even if they were not subjected to a remote tensile stress (Figure 6.9b). In rocks, as the compressive stress increases, the tensile stress at the tips of cracks exceeds the strength of the rock, and the crack propagates parallel to the compressive stress direction.
In the compressive stress environment illustrated in Figure 3.9, the confining pressure required is very small; but tensile cracks can also be generated in a rock cylinder when the remote stress is compressive under higher confining pressure when adding fluid pressure in pores and cracks of the sample (i.e., the pore pressure). The uniform, outward push of a fluid in a microcrack can have the effect of creating a local tensile stress at crack tips, and thus can cause a crack to propagate. We call this process hydraulic fracturing. As soon as the crack begins to grow, the volume of the crack increases, so if no additional fluid enters the crack, the fluid pressure decreases. Crack propagation ceases when pore pressure drops below the value necessary to create a sufficiently large tensile stress at the crack tip, and does not begin again until the pore pressure builds up sufficiently. Therefore, tensile cracking driven by an increase in pore pressure typically occurs in pulses. We’ll return to the role of hydraulic fracturing later in this chapter.
|
|
FIGURE 3.9. (a) A cross section showing a rock cylinder with mesoscopic cracks formed by the process of longitudinal splitting. (b) A simple “envelope” model of longitudinal splitting. If you push down on the top of an envelope (whose ends have been cut off), the sides of the envelope will move apart. [6.9]
|
Modes of Crack-Surface Displacement
Before leaving the subject of Griffith cracks, we need to address one more critical issue, namely, the direction in which an individual crack grows when it is loaded. So far we have limited ourselves to cracks that are perpendicular to a remote stress. But what about cracks in other orientations with respect to stress, and how do they propagate? Materials scientists identify three configurations of crack loading. These configurations result in three different modes of crack-surface displacement (Figure 3.10). Note that the “displacement” we are referring to when describing crack propagation is only the infinitesimal movement initiating propagation of the crack tip and is not measurable mesoscopic displacement as in faults.
|
|
|
FIGURE 3.10. Block diagrams illustrating the three modes of crack surface displacement: (a) Mode I, (b) Mode II, (c) Mode III. Mode I is a tensile crack, and Mode II and Mode III are shear-mode cracks. [6.11] |
During Mode I displacement (tensile mode), a crack opens very slightly in the direction perpendicular to the crack sur- face, so Mode I cracks are tensile cracks. They form parallel to the principal plane of stress that is perpendicular to the σ3 direction, and can grow in their plane without changing orientation. During Mode II displacement (the sliding mode), rock on one side of the crack surface moves very slightly in the direction parallel to the fracture surface and perpendicular to the fracture front. During Mode III displacement (the tearing mode), rock on one side of the crack slides very slightly parallel to the crack but in a direction parallel to the fracture front.
Although shear-mode cracks appear similar to mesoscopic faults, Mode II and Mode III cracks are not simply microscopic equivalents of faults. We realize the difference when we examine the propagation of shear-mode cracks. As they start growing, shear-mode cracks immediately curve into the orientation of tensile or Mode I cracks, meaning that shear-mode cracks do not grow in their plane. Propagating shear-mode cracks spawn new tensile cracks, called wing cracks, a process illustrated in Figure 3.11.
|
|
FIGURE 3.11. Propagating shear-mode crack and the formation of wing cracks. (a) A tensile stress concentration occurs at the ends of a Mode II crack that is being loaded. (b) Mode I wing cracks form in the zones of tensile-crack concentration. [6.12]
|
FORMATION OF SHEAR FRACTURES
Shear fractures differ markedly from tensile cracks. A shear fracture is a surface across which a rock loses continuity when the shear stress parallel to the surface is sufficiently large. Shear fractures are initiated in laboratory rock cylinders at a typical angle of about 30° to σ1 under conditions of confining pressure (σ1 > σ2 = σ3). Because there is a component of normal stress acting on the fracture in addition to shear stress, friction resists sliding on the fracture during its formation. If the shear stress acting on the fracture continues to exceed the frictional resistance to sliding, the fracture grows and displacement accumulates. Shear fractures (or faults) are therefore not simply large shear-mode cracks, because, as we have seen, shear-mode cracks cannot grow in their own plane. This conceptual difference is very important.
So how do shear fractures form? We can gain insight into the process of shear-fracture formation by generating shear ruptures during a laboratory triaxial loading experiment, using a rock cylinder under confining pressure. So to begin our search for an answer to this question, we first examine such an experiment. In a confined-compression triaxial-loading experiment, we take a cylinder of rock, jacket it in copper or rubber, surround it with a confining fluid in a pressure chamber, and squeeze it between two hydraulic pistons. In the experiment shown in Figure 3.12, the rock itself stays dry. During the experiment, we apply a confining pressure (σ2 = σ3) to the sides of the cylinder by increasing the pressure in the surrounding fluid, and an axial load (σ1) to the ends of the cylinder by moving the pistons together at a constant rate. By keeping the value of σ3 constant while σ1 gradually increases, we increase the differential stress (σd = σ1 – σ3). In this experiment we measure the magnitude of σd, the change in length of the cylinder (which is the axial strain, ea), and the change in volume (Δ) of the cylinder.
A graph of σd versus ea (Figure 3.12a) shows that the experiment has four stages. In Stage I, we find that as σd increases, ea also increases and that the relationship between these two quantities is a concave-up curve. In Stage II of the experiment, the relationship between σd and ea is a straight line with a positive slope. During Stage I and most of Stage II, the volume of the sample decreases slightly. In Stage III of the experiment, the slope of the line showing the relation between σd and ea decreases. The stress at which the curve changes slope is called the yield strength. During the latter part of Stage II and all of Stage III, we observe a slight increase in volume, a phenomenon known as dilatancy, and if we had a very sensitive microphone attached to the sample during this time, we would hear lots of popping sounds that reflect the formation and growth of microcracks. Suddenly, when σd equals the failure stress (σf), a shear rupture surface develops at an angle of about 30° to the cylinder axis, and there is a stress drop. A stress drop in this context means that the axial stress supported by the specimen suddenly decreases and large strain accumulates at a lower stress. To picture this stress drop, imagine that you’re pushing a car that is stuck in a ditch. You have to push hard until the tires come out of the ditch, at which time you have to stop pushing so hard, or you will fall down as the car rolls away. The value of σd at the instant that the shear rupture forms and the stress drops is called the failure strength for shear rupture. Once failure has occurred, the sample is no longer intact and frictional resistance to sliding on the fracture surface determines its further behavior.
|
|
|
FIGURE 3.12. Fracture formation. (a) Stress–strain plot (differential stress versus axial shortening) showing stages (I–IV) in a confined compression experiment. The labels indicate the process that accounts for the slope of the curve. (b) The changes in volume accompanying the axial shortening illustrate dilatancy; left of the dashed line, the sample volume decreases, whereas to the right of the dashed line the sample volume increases. (c–f) Schematic cross sections showing the behavior of rock cylinders during the successive stages of a confined compression experiment and accompanying stress–strain plot, emphasizing the behavior of Griffith cracks (cracks shown are much larger than real dimensions). (c) Pre-deformation state, showing open Griffith cracks. (d) Compression begins and volume decreases due to crack closure. (e) Crack propagation and dilatancy (volume increase). (f) Merging of cracks along the future throughgoing shear fracture, followed by loss of cohesion of the sample (mesoscopic failure). [6.14] |
What physically happened during this experiment? During Stage I, preexisting open microcracks underwent closure. During Stage II, the sample underwent elastic shortening parallel to the axis, and because of the Poisson effect expanded slightly in the direction perpendicular to the axis (Figure 6.14d). The Poisson effect refers to the phenomenon in which a rock that is undergoing elastic shortening in one direction extends in the direction at right angles to the shortening direction. The ratio between the amount of shortening and the amount of extension is Poisson’s ratio, ν [Note: as Poisson’s ratio has the unit length/length, it is dimensionless; a typical value of ν for rocks is 0.25]. At the start of Stage III, tensile microcracks begin to grow throughout the sample, and wing cracks grow at the tips of shear-mode cracks. The initiation and growth of these cracks causes the observed slight increase in volume, and accounts for the popping noises (Figure 3.12e). During Stage III, the tensile cracking intensifies along a narrow band that cuts across the sample at an angle of about 30° to the axial stress. Failure occurs in Stage IV when the cracks self-organize to form a throughgoing surface along which the sample loses continuity, so that the rock on one side can frictionally slide relative to the rock on the other side (Figure 3.12f). As a consequence, the cylinders move together more easily and stress abruptly drops.
The fracture development scenario described above shows that the failure strength for shear fracture is not a definition of the stress state at which a single crack propagates, but rather it is the stress state at which a multitude of small cracks coalesce to form a throughgoing rupture. Also note that two ruptures form in some experiments, both at ∼30° to the axial stress, as we’ll explore later. The angle between these conjugate fractures is ∼60°, and the acute bisector is parallel to the maximum principal stress. With continued displacement, however, it is impossible for both fractures to remain active, because displacement on one fracture will offset the other. Thus, typically only one fracture will evolve into a throughgoing fault (see below).
Shear Failure Criteria and Failure Envelopes
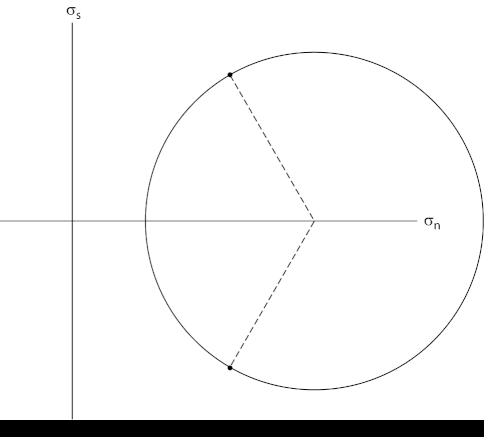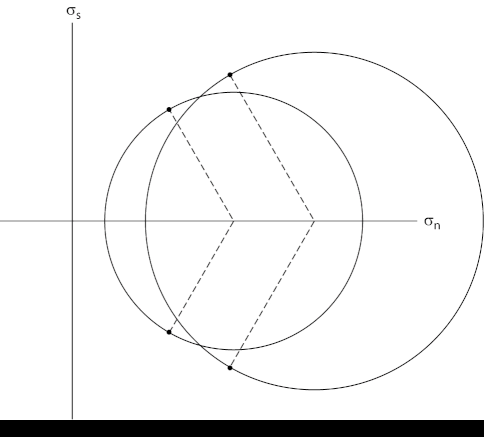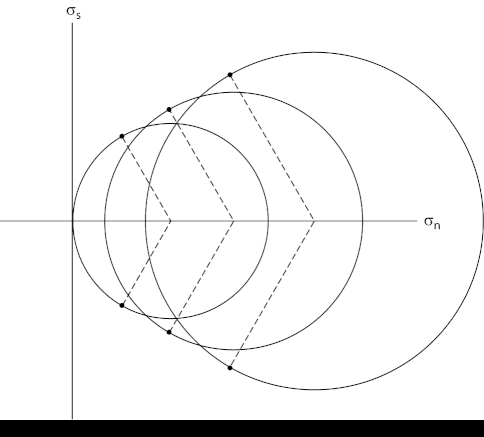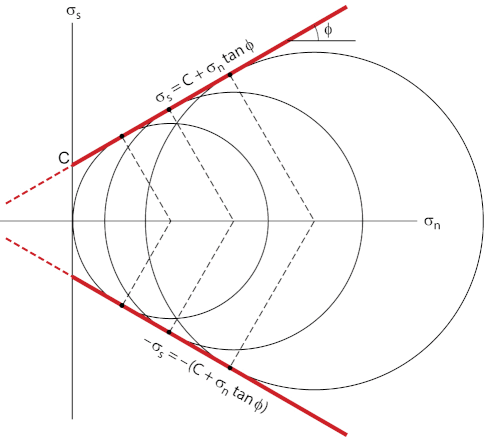
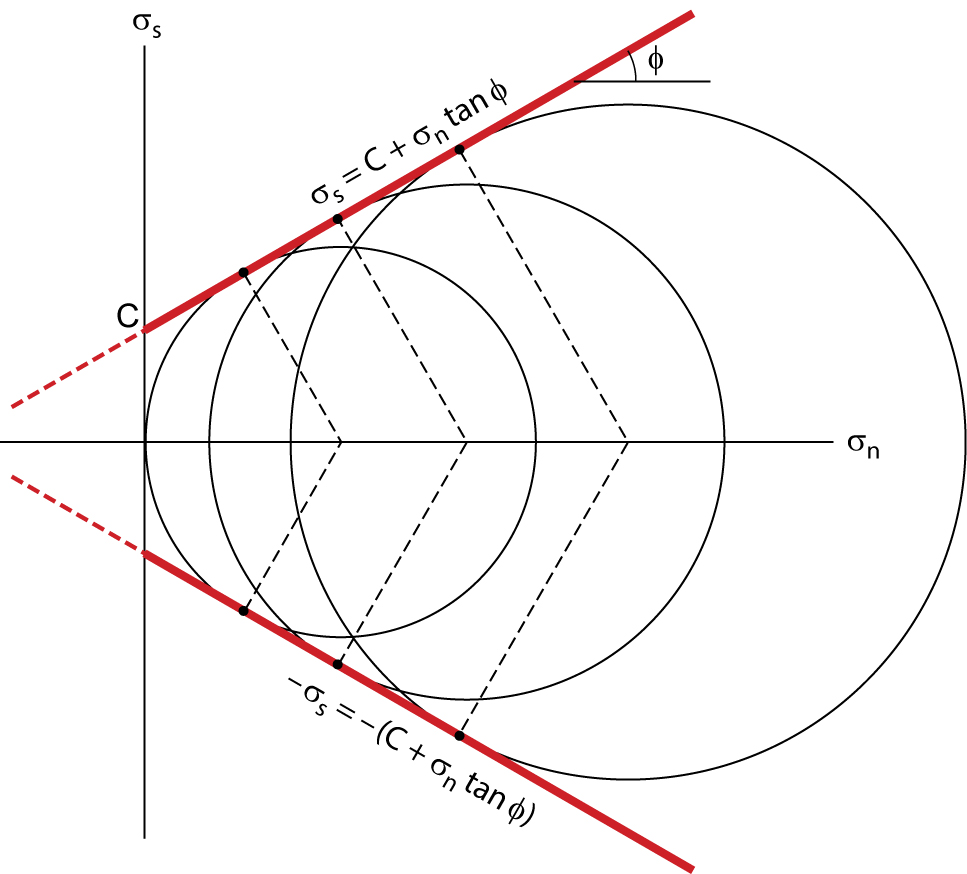
A shear-fracture criterion is an expression that describes the stress state at which a shear rupture forms and separates a sample into two pieces. Because shear-fracture initiation in a laboratory sample inevitably leads to failure of the sample, meaning that after rupture the sample can no longer support a load that exceeds the frictional resistance to sliding on the fracture surface, shear-rupture criteria are also commonly known as shear-failure criteria. Charles Coulomb[3] was one of the first to propose a shear-fracture criterion. He suggested that if all the principal stresses are compressive, as is the case in a confined compression experiment, a material fails by the formation of a shear fracture, and that the shear stress parallel to the fracture surface, at the instant of failure, is related to the normal stress by the equation:
σs = C + μ . σn Eq 3.5
where σs is the shear stress parallel to the fracture surface at failure; C is the cohesion of the rock, a constant that specifies the shear stress necessary to cause failure if the normal stress across the potential fracture plane equals zero; σn is the normal stress across the shear fracture at the instant of failure; and μ is a constant traditionally known as the coefficient of internal friction. The name for μ originally came from studies of friction between grains in unconsolidated sand and of the control that such friction has on slope angles of sand piles, so the name is essentially meaningless in the context of shear failure of a solid rock; μ should be viewed simply as a constant of proportionality. Equation 6.6, also known as Coulomb’s failure criterion, basically states that the shear stress necessary to initiate a shear fracture is proportional to the normal stress across the fracture surface.
The Coulomb criterion plots as a straight line on a Mohr diagram (Figure 3.13; see also Chapter 2). To see this, let’s plot the results of four triaxial loading experiments in which we increase the axial load on a confined granite cylinder until it ruptures. In the first experiment, we set the confining pressure (σ2 = σ3) at a relatively low value, increase the axial load (σ1) until the sample fails, and then plot the Mohr circle representing this critical stress state, meaning the stress state at the instant of failure, on the Mohr diagram. When we repeat the experiment, using a new cylinder, and starting at a higher confining pressure, we find that as σ3 increases, the differential stress (σ1 – σ3) at the instant of failure also increases. Thus, the Mohr circle representing the second experiment has a larger diameter and lies to the right of the first circle. When we repeat the experiment two more times and plot the four circles on the diagram, we find that they are all tangent to a straight line with a slope of μ (i.e., tan φ) and a y-intercept of C, and this straight line is the Coulomb criterion. Note that we can also draw a straight line representing the criterion in the region of the Mohr diagram below the σn-axis.
|
FIGURE 3.13. Mohr diagram with a Coulomb failure envelope (red) based on a series of compression experiments with decreasing differential stress. The circles represent differential stress states at the instant of faulting and the dots represent failure planes. The failure envelope is represented by two straight lines (red) that connect the dots (failure planes). [6.15] |
A line drawn from the center of a Mohr circle to the point of its tangency with the Coulomb criterion defines 2θ, where θ is the angle between the σ3 direction and the plane of shear fracture (typically about 30°). Because the Coulomb criterion is a straight line, this angle is constant for the range of confining pressures for which the criterion is valid. The reason for the 30° angle becomes evident in a graph plotting normal stress magnitude and shear stress magnitude as a function of the angle between the plane and the σ1 direction (Figure 3.14). Notice that the minimum normal stress does not occur in the same plane as the maximum shear stress. Shear stress is at its highest on a potential failure plane oriented at 45° to σ1, but the normal stress across this potential plane is still too large to permit shear fracturing in planes of this orientation. The shear stress is a bit lower across a plane oriented at 30° to σ1, but is still fairly high. However, the normal stress across the 30° plane is substantially lower, favoring shear-fracture formation.
|
|
FIGURE 3.14. The change in magnitudes of the normal and shear components of stress acting on a plane as a function of the angle α between the plane and the σ1 direction; the angle θ = 90 – α is plotted for comparison with other diagrams. At point 1 (α = θ = 45°), shear stress is a maximum, but the normal stress across the plane is quite large. At point 2 (θ = 60°, α=30°), the shear stress is still quite high, but the normal stress is much lower. [6.16]
|
Coulomb’s criterion is an empirical relation, meaning that it is based on experimental observation alone, not on theoretical principles or knowledge of atomic scale or crystal-scale mechanisms. This failure criterion does not relate the stress state at failure to physical parameters, as does the Griffith criterion, nor does it define the state of stress in which the microcracks, which eventually coalesce to form the shear rupture, begin to propagate. The Coulomb criterion does not predict whether the fractures that form will dip to the right or to the left with respect to the axis of the rock cylinder in a triaxial loading experiment. In fact, as mentioned earlier, conjugate shear fractures, one with a right-lateral shear sense and one with a left lateral shear sense, may develop (Figure 3.15). The two fractures, typically separated by an angle of ∼60°, correspond to the tangency points of the circle representing the stress state at failure with the Coulomb failure envelope.
|
|
FIGURE 3.15. Cross-sectional sketch showing how only one of a pair of conjugate shear fractures (a) evolves into a single fault with measurable displacement (b). [6.17] |
The German engineer Otto Mohr conducted further studies of shear-fracture criteria and found that Coulomb’s straight-line relationship only works for a limited range of confining pressures. He noted that at lower confining pressure, the line representing the stress state at failure curved with a steeper slope, and that at higher confining pressure, the line curved with a shallower slope (Figure 3.16). Mohr concluded that over a range of confining pressure, the failure criteria for shear rupture resembles a portion of a parabola lying on its side, and this curve represents the Mohr-Coulomb criterion for shear fracturing. Notice that this criterion is also empirical. Unlike Coulomb’s straight-line relation, the change in slope of the Mohr- Coulomb failure envelope indicates that the angle between the shear fracture plane and σ1 actually does depend on the stress state. At lower confining pressures, the angle is smaller, and at high confining pressures, the angle is steeper.
|
|
FIGURE 3.16. Mohr failure envelope. Moving toward the σs-axis and into the extensional field (dashed line segments in Fig 3.13), the slope of the envelope (red) steepens. Therefore, the value of α (the angle between fault and σ1) becomes smaller (compare 2α1, 2α2, and 2α3), meaning that the fracture plane becomes parallel to σ1 in extension (longitudinal splitting). [6.18]
|
The Mohr-Coulomb criterion (both for positive and negative values of σs) defines a failure envelope on the Mohr diagram. A failure envelope separates the field on the diagram in which stress states are stable from the field in which stress states are unstable (Figure 3.17). By this definition, a stable stress state is one that a sample can withstand without undergoing brittle failure. An unstable stress state is an impossible condition to achieve, for the sample will have failed by fracturing before such a stress state is reached (Figure 6.19). In other words, a stress state represented by a Mohr circle that lies entirely within the envelope is stable, and will not cause the sample to develop a shear rupture. A circle that is tangent to the envelope specifies the stress state at which brittle failure occurs. Stress states defined by circles that extend beyond the envelope are unstable, and are therefore impossible within the particular rock being studied.
|
|
|
FIGURE 3.17. (a) A brittle failure envelope as depicted on a Mohr diagram. Within the envelope (shaded area), stress states are stable, but outside the envelope, stress states are unstable. (b) A stress state that is stable. The Mohr circle, which passes through values for σ1 and σ3 and defines the stress state, falls entirely inside the envelope. (c) A stress state at the instant of failure. The Mohr circle touches the envelope. (d) A stress state that is impossible, since the rock would have fractured by then. [6.19] |
Can we define a failure envelope representing the critical stress at failure for very high confining pressures, very low confining pressures, or for conditions where one of the principal stresses is tensile? Let's look at each of these conditions separately. At high confining pressures, samples may begin to deform plastically. Under such conditions, we are no longer really talking about brittle deformation, so the concept of a failure envelope no longer really applies. However, we can approximately represent the yield envelope, meaning the stress state at which the sample begins to yield plastically, on a Mohr diagram by a pair of lines that parallel the σn-axis (Figure 3.18). This yield condition, known as Von Mises criterion, indicates that plastic yielding is effectively independent of the differential stress (and thus shear stress), once the yield stress has been achieved.
|
|
FIGURE 3.18. Mohr diagram illustrating the Von Mises yield criterion. Note that the criterion is represented by two lines that parallel the σn-axis. [6.20]
|
Taking all of the above empirical criteria into account, we can construct a composite failure envelope that represents the boundary between stable and unstable stress states for a wide range of confining pressures and for conditions for which one of the principal stresses is tensile (Figure 3.19).
|
|
|
|
FIGURE 3.19. (a) A representative composite failure envelope on a Mohr diagram. The different parts of the envelope are labeled, and are discussed in the text. (b) Sketches of the fracture geometries that form during failure. Note that the geometry depends on the part of the failure envelope that represents failure conditions, because the slope of the envelope is not constant. Note the change in angle of fracture and σ1. [6.21] |
|
The composite failure envelope roughly resembles a cross section of a cup lying on its side. The various parts of the curve are labeled. Starting at the right side of the diagram, we have Von Mises criteria, represented by horizontal lines. (Remember that the Von Mises portion of the envelope is really a plastic yield criterion, not a brittle failure criterion.) The portion of the curve where the lines begin to slope effectively represents the frictional–plastic transition. To the left of the brittle–plastic transition, the envelope consists of two straight sloping lines, representing Coulomb’s criterion for shear rupturing. For failure associated with the Coulomb criterion, remember that the angle between the shear rupture and the σ1 direction is independent of the confining pressure. Closer to the σs-axis, the slope of the envelope steepens, and the envelope resembles a portion of a parabola. This parabolic part of the curve represents Mohr’s criterion, and for failure in this region, the decrease in the angle between the fracture and the σ1 direction depends on how far to the left the Mohr circle touches the failure curve. The part of the parabolic envelope with steep slopes specifies failure criteria for supposed transitional tensile fractures formed at a very small angle to σ1, but as we discussed, the existence of such fractures remains controversial. The point where the envelope crosses the σn-axis represents the failure criterion for tensile cracking, but as we have discussed, this criterion really shouldn’t be specified by a point, for the tensile strength of a material depends on the dimensions of the flaws it contains. Note that for a circle tangent to the composite envelope at T0, 2θ = 180 (or, α = 0), so the fracture that forms is parallel to σ1! Also, note that there is no unique value of differential stress needed to cause tensile failure, as long as the magnitude of the differential stress (the diameter of the Mohr circle) is less than about 4T0, for this is the circle whose curvature is the same as that of the apex of the parabola.
STRESS AND FAULT TYPES: ANDERSON’S THEORY
Different fault types occur in nature, including reverse, normal and lateral slip (Figure 3.20). Why? Faulting represents a response of rock to shear stress, so it only occurs when the differential stress (σd = σ1 – σ3 = 2σs) does not equal zero. Because the shear-stress magnitude on a plane changes as a function of the orientation of the plane with respect to the principal stresses, we should expect a relationship between the orientation of faults formed during a tectonic event and the trajectories of principal stresses during that event. Indeed, faults that initiate as Coulomb shear fractures will form at an angle of about 30° to the σ1 direction and contain the σ2 direction. This relationship is called Anderson’s theory of faulting[4]. Why isn’t σ1 at 45° to the fault planes, where the shear stress is maximum? Recall the role of the normal stress, where the ratio of shear stress to normal stress on planes orientated at about 30° to σ1 is at a maximum (see Chapter 2).
|
|
|
|
FIGURE 3.20. Field photographs of end-member fault types. (a) Normal faults; (b) high-angle reverse faults; (c) lateral- or strike-slip fault (San Andreas fault near San Luis Opisbo (CA). GE 35°07'23.75" N 119°39'25.26" W. |
|
The Earth’s surface is a “free surface” (the contact between ground and air/fluid) that cannot, therefore, transmit a shear stresses (recall earthquake S-waves). Therefore, regional principal stresses are parallel or perpendicular to the surface of the Earth in the upper crust. Considering that gravitational body force is a major contributor to the stress state, and that this force acts vertically, stress trajectories in homogeneous, isotropic crust can maintain this geometry at depth. Anderson’s theory of faulting states that in the Earth-surface reference frame, normal faulting occurs where σ2 and σ3 are horizontal and σ1 is vertical, thrust faulting occurs where σ1 and σ2 are horizontal and σ3 is vertical, and strike-slip faulting occurs where σ1 and σ3 are horizontal and σ2 is vertical (Figure 3.21). Moreover, the dip of thrust faults should be ∼30°, the dip of normal faults should be ∼60°, and the dip of strike-slip faults should be about vertical. For example, if the σ1 orientation at convergent margins is horizontal, Anderson’s theory predicts that thrust faults should form in this environment, and indeed belts of thrust faults form in collisional mountain belts.
|
|
|
FIGURE 3.21. Anderson’s theory of faulting predicts (a) (high-angle) normal faults, (b) (low-angle) reverse faults (or thrusts), and (c) (vertical) strike-slip faults. [8.27] |
Anderson’s theory is a powerful tool for regional analysis, but we cannot use this theory to predict all fault geometries in the Earth’s crust for several reasons. First, faults do not necessarily initiate in intact rock. The frictional sliding strength of a preexisting surface is less than the shear failure strength of intact rock; thus, preexisting joint surfaces or faults may be reactivated before new faults initiate, even if the preexisting surfaces are not inclined at 30° to σ1 and do not contain the σ2 trajectory. Preexisting fractures that are not ideally oriented with respect to the principal stresses become oblique-slip faults. Second, a fault surface is a material feature in a rock body whose orientation may change as the rock body containing the fault undergoes progressive deformation. Thus, the fault may rotate into an orientation not predicted by Anderson’s theory. Local stress trajectories may be different from regional stress trajectories because of local heterogeneities and weaknesses (e.g., contacts between contrasting lithologies, preexisting faults) in the Earth’s crust. As a consequence, local fault geometry might not be geometrically related to regional stresses. Third, systematic changes in stress trajectories are likely to occur with depth in mountain belts (e.g., along a regional detachment), but Anderson’s theory assumes that the stress field is homogeneous and that the principal stresses are either horizontal or vertical, regardless of depth.
Andersonian theory also offers a major insight into stress states for faulting. Because the vertical stress equals the lithostatic pressure, both horizontal stresses are large in reverse faulting, where 3 is vertical, one horizontal stress is large and the other small in lateral-slip faulting, where 2 is vertical and both horizontal stress are relatively small in normal faulting, where 1 is vertical. As a consequence the differential stresses needed for reverse, lateral slip and normal faulting of rock, respectively is progressively smaller. We return to this later in the chapter.
FRICTIONAL SLIDING
So far we have examined the formation of a throughgoing fault, but what about continued displacement after a fault has been created? Movement on preexisting surfaces is the focus of friction, which is the resistance to sliding on a surface. Frictional sliding refers to the movement on a surface that takes place when shear stress parallel to the surface exceeds the frictional resistance to sliding. The principles of frictional sliding were formulated hundreds of years ago. We do a simple experiment that produces, at first, counterintuitive behavior (Figure 3.22).
|
|
FIGURE 3.22. Frictional sliding of objects with same mass, but with different (apparent) contact areas. The friction coefficients and, therefore, sliding forces (Ff) are equal for both objects, regardless of (apparent) contact area. The ratio of frictional force and load force is the friction coefficient, µ. [6.22]
|
Attach a spring to a beam of wood that is placed on a table with the flat side down. Pull the spring until the beam slides. Now place the beam on its narrow side and repeat the experiment. Surprisingly, the spring extends by the same amount before beam sliding occurs, irrespective of the area of contact. Similar experiments led to what are often called Amontons’[5] laws of friction:
- Frictional force is a function of normal force.
- Frictional force is independent of the (apparent) area of contact (in his words, “the resistance caused by rubbing only increases or diminishes in proportion to greater or lesser pressure [load] and not according to the greater or lesser extent of the surfaces”).
- Frictional force is mostly independent of the material used (in his words, “the resistance caused by rubbing is more or less the same for iron, lead, copper and wood in any combination if the surfaces are coated with pork fat”).
Let’s explore the reason for this behavior, which has important consequences for natural faulting processes and earthquake mechanics. Note that we can distinguish between static friction, which is associated with first motion (associated with Coulomb failure), and dynamic friction, which is associated with continued motion. Friction exists because no real surface in nature, no matter how finely polished, is perfectly smooth. The bumps and irregularities which protrude from a rough surface are called asperities (Figure 3.23a). When two surfaces are in contact, they touch only at the asperities, and the asperities of one surface may indent or sink into the face of the opposing surface (Figure 3.23b). The cumulative area of the asperities that contact the opposing face is the real area of contact (Ar in Figure 3.23c). In essence, asperities act like an anchor holding a ship in place. In order for the ship to drift, either the anchor chain must break, or the anchor must drag along the sea floor. Similarly, in order to initiate sliding of one rock surface past another, it is necessary either for asperities to break off, or for them to plow a furrow or groove into the opposing surface.
|
|
|
FIGURE 3.23. Concept of asperities and the real area of contact (Ar). (a) Schematic cross-sectional close-up showing the irregularity of a fracture surface and the presence of voids and contact areas (asperities) along the surface. (b) Idealized asperity model showing the consequence of increasing the load (normal force) that increases the real area of contact (Ar). (c) Map of a fracture surface; the red areas are real areas of contact that increase or shrink as a function of greater or smaller load, respectively. [6.23] |
The stress necessary to break off an asperity or to cause it to plow depends on the real area of contact, so, as the real area of contact increases, the frictional resistance to sliding (that is, the force necessary to cause sliding) increases. Again, considering our ship analogy, it takes less wind to cause a ship with a small anchor to drift than it does to cause the same-sized ship with a large anchor to drift. Thus, the frictional resistance to sliding is proportional to the normal force component across the surface, because of the relation between real area of contact and friction. An increase in the normal force (load) pushes asperities into the opposing wall more deeply, causing an increase in the real area of contact. Returning to our earlier experiment with a sliding beam, we can now understand that the object’s mass, rather than the (apparent) area of contact (the side of the beam), determines the ability to slide.
Frictional Sliding Criteria
Because of friction, a certain critical shear stress must be achieved in a rock before frictional sliding is initiated on a preexisting fracture, and a relation defining this critical stress is the failure criterion for frictional sliding. Experimental work shows that failure criteria for frictional sliding, just like the Coulomb failure criterion for intact rock, plot as sloping straight lines on a Mohr diagram. A compilation of friction data from a large number of experiments, using a great variety of rocks (Figure 3.24), shows that the failure criterion for frictional sliding is basically independent of rock type, called Byerlee’s law[6]:
σs/σn = constant = coefficient of friction (µ) Eq. 3.6
|
|
FIGURE 3.24. Graph of shear stress and normal stress values at the initiation of sliding on preexisting fractures in a variety of rock types. The best-fit line defines Byerlee’s law, which is defined for two regimes (blue lines), or can be fitted by one line (red). [6.24]
|
The empirical relationship between normal and shear stress that best fits the observations, known as Byerlee’s law depends on the value of σn. For σn < 200 MPa, the best-fitting criterion is a line described by the relationship σs = 0.85σn, whereas for 200 MPa < σn < 2000 MPa, the best-fitting criterion is a line described by the equation σs = 50 MPa + 0.6σn. The proportionality between normal and shear stress is, as before, called the friction coefficient, which is ~0.75 when fitting a single line [Note: technically, this is called the static friction coefficient].
Will New Fractures Form or Will Existing Fractures Slide?
Failure envelopes allow us to quickly determine whether it is more likely that an existing shear rupture will slip in a sample, or that a new shear rupture will form (Figure 3.25). For example, look at Figure 3.25b, which shows both the Byerlee’s frictional sliding envelope and the Coulomb shear fracture envelope for natural dolomite. Note that the slope and intercept of the two envelopes are different, so that for a specific range of preexisting fracture orientations, the Mohr circle representing the stress state at failure touches the frictional envelope before it touches the fracture envelope, meaning the preexisting fracture slides before a new fracture forms.
|
|
|
FIGURE 3.25. (a) Mohr diagram based on experiments with Blair dolomite, showing how a single stress state (Mohr circle) would contact the frictional sliding envelope before it would contact the Coulomb envelope (heavy line). Surface A in (b) is the Coulomb shear fracture that would form in an intact rock. However, sliding would occur on surfaces between intersections with the friction envelope (marked by shaded area for friction envelope μ = 0.85) before new fracture initiation. Preexisting surfaces B to E are surfaces that will slide with decreasing friction coefficients. Consider the geologic relevance of decreasing friction coefficients for stress state, failure, and fracture orientation. [6.25] |
However, preexisting fractures do not always slide before a new fracture is initiated. Confined compression experiments indicate that if the preexisting fracture is oriented at a high angle to the σ1 direction (generally > 75°; plane E in Figure 6.25), the normal stress component across the discontinuity is so high that friction resists sliding, and it is actually easier to initiate a new shear fracture at a smaller angle to σ1 (plane B in Figure 3.25). Sliding then occurs on the new fracture. If a preexisting fracture is at a very small angle to σ1 (generally < 15°; plane A in Figure 3.25), the shear stress on the surface is relatively low, so again it ends up being easier to initiate a new shear fracture than to cause sliding on a preexisting weak surface. Thus, preexisting planes whose angles to σ1 are between 15° and 75° probably will be reactivated before new fractures form.
LIMITING STRESSES FOR SLIDING
The question of how large the shear stress (σs) must be in order to initiate faults or to reactivate preexisting faults remains highly controversial. The magnitude of σs necessary to trigger faulting depends on fluid pressure, lithology, strain rate, temperature, and the orientation of the preexisting fault. Recall that for a given range of orientations, the stress necessary to initiate frictional sliding on a preexisting fault is less than that necessary to initiate a new fault. Rock mechanics experiments provide one avenue of approach into this problem. From laboratory triaxial loading experiments, we determine that, all other factors being equal, the shear stress for failure increases as confining pressure increases, and that σs is greatest for contractional faulting and least for extensional faulting. Limiting stress conditions for sliding each of the three fault types can be determined from Andersonian conditions (representative vertical stress equals lithostatic pressure, ρ⋅g⋅h; Figure 3.21), equations for n and s (Chapter 2) and the ratio (s/n = , friction coefficient). Without showing the details we get the relationship:
1 = 3 . [2+1)1/2 + ]2 Eq. 3.7
and
(σ1 – σ3) ≥ β (ρ ⋅ g ⋅ z) Eq. 3.8
From the friction coefficient we determine β, which is 3, 1.2, and 0.75 for reverse, strike-slip, and normal faulting, respectively, using a value =0.75 (friction law; Figure 3.24). These limiting stresses are plotted in Figure 3.26 as a function of differential stress and depth (pressure) for each of the three fault types. Stress measurements at or above its line means that sliding would occur for a respective fault condition.
|
|
FIGURE 3.26. Graph showing variation in differential stress necessary to initiate sliding on reverse, strike-slip, and normal faults, as a function of depth. The relationship is given by Equation 8.1, assuming a friction coefficient, μ=0.75, and a fluid pressure parameter, λ=0 (no fluid present) and λ = 0.9 (fluid pressure is 90% of lithostatic pressure). [8.30]
|
Geologists have questioned the validity of stress estimates based on laboratory studies, because of uncertainty about how such estimates scale up to crustal dimensions and about time-dependent changes. Thus, alternative approaches have been used to determine stress magnitudes for crustal-scale faulting, including analysis of heat generation during faulting, direct measurement of stresses near faults, and borehole data.
ROLE OF FLUIDS
All natural rocks of the crust contain pores and cracks. We’ve already seen how important these are in the process of brittle failure. In the upper crust of the Earth below the water table, these spaces, which constitute the porosity of rock, are filled with fluid. This fluid is most commonly water, though in some places it is oil or gas. If there is a high degree of permeability in the rock, meaning that water can flow relatively easily from pore to pore and/or in and out of the rock layer, then the pressure in a volume of pore water at a location in the crust is roughly hydrostatic, meaning that the pressure reflects the weight of the overlying water column (Figure 3.27).
|
|
FIGURE 3.27. Graph of lithostatic (brown) versus hydrostatic (blue) pressure as a function of depth in the Earth’s crust. [6.26]
|
Fluid pressure is determined by the relationship Pf = ρ ⋅ g ⋅ h, where ρ is the density of water (1000 kg/m3), g is the gravitational constant (9.8 m/s2), and h is the depth. Pore pressure, which is the fluid pressure exerted by fluid within the pores of a rock, may exceed the hydrostatic pressure if rock permeability is restricted. For example, the fluid trapped in a sandstone lens surrounded by impermeable shale cannot escape, so the pore pressure in the sandstone can approach or even equal lithostatic pressure (Pl), meaning that the fluid pressure approaches the weight of the overlying column of rock (i.e., Pf = Pl = ρ ⋅ g ⋅ h, where ρ = 2,500–3,000 kg/m3). Note that rock, on average, is two to three times denser than water. When the fluid pressure in pore water exceeds hydrostatic pressure, we say that the fluid is overpressured.
How does pore pressure affect the failure strength of rock? The pore pressure is an outward push that opposes inward compression from the rock, so the fluid supports part of the applied load. If pore pressure exceeds the least compressive stress (σ3) in the rock, tensile stresses at the tips of cracks oriented perpendicularly to the σ3 direction become sufficient for the crack to propagate. In other words, pore pressure in a rock can cause tensile cracks to propagate, even if none of the remote stresses are tensile, because pore pressure can induce a crack-tip tensile stress that exceeds the magnitude of σ3. This process is called hydraulic fracturing or fracking. On a Mohr diagram, it can be represented by movement of Mohr’s circle to the left (Figure 3.28). Note that rocks do not have to be overpressured in order for natural hydraulic fracturing to occur, but Pf must equal or exceed the magnitude of the smallest principal stress (σ3).
|
|
FIGURE 3.28. A Mohr diagram showing how an increase in pore pressure moves the Mohr circle toward the origin. The increase in pore pressure decreases the mean stress (σmean), but does not change the magnitude of differential stress (σ1 – σ3). In other words, the diameter of the Mohr circle remains constant, but its center moves to the left. [6.27]
|
Effect of Pore Pressure on Failure
We can observe the effects of pore pressure on shear fracturing by running a confined compression experiment in which we pump fluid into the sample through a hole in one of the pistons, thereby creating a fluid pressure, Pf, in pores of the sample (Figure 3.29). The fluid creating the confining pressure acting on the sample is different from and is not connected to the fluid inside the sample. The magnitude of Pf decreases the confining pressure (σ3) and σ1 by the same amount. So if the pore pressure increases in the sample, the mean stress decreases but the differential stress remains the same.
|
|
FIGURE 3.29. Cross-sectional sketch illustrating a rock cylinder (brown) in a triaxial loading experiment. Fluid has access to the rock cylinder and fills the cracks. (b) A fluid-filled crack that is being pushed apart from within by pore-fluid pressure. [6.10]
|
This effect can be represented by the Coulomb failure criterion equation; Pf decreases the magnitude of σn on the right side of the equation:
σs = C + μ . (σn – Pf) Eq. 3.9
The term (σn – Pf) is often labeled σn*, and is called the effective normal stress.
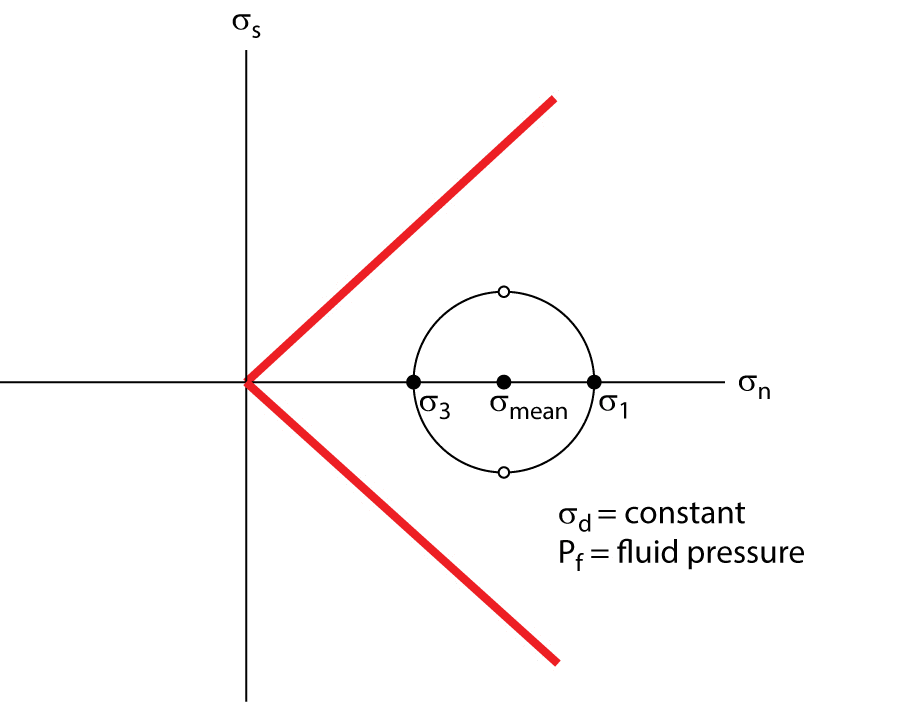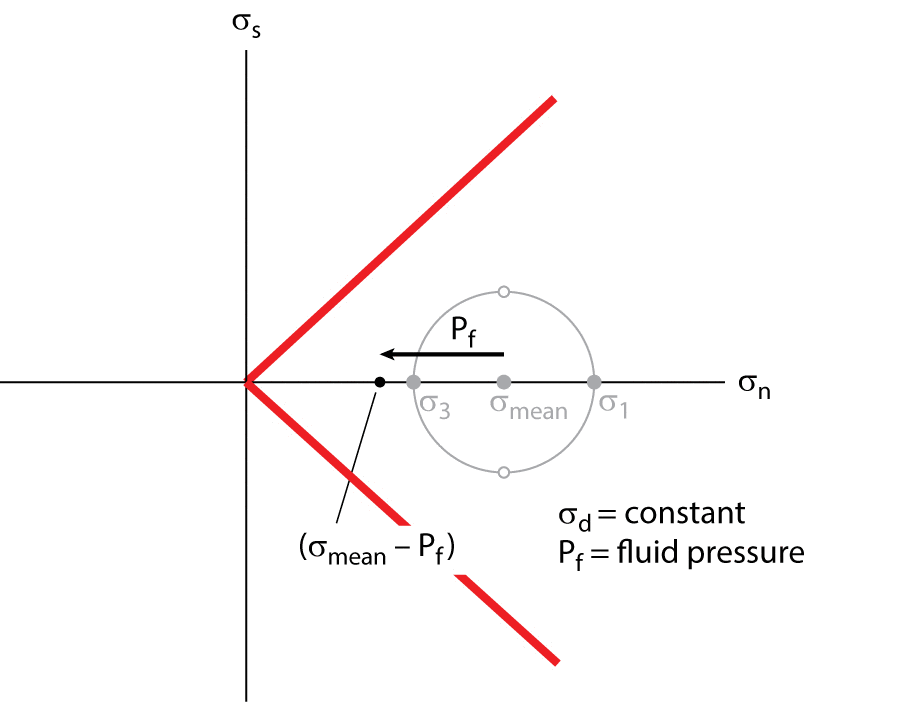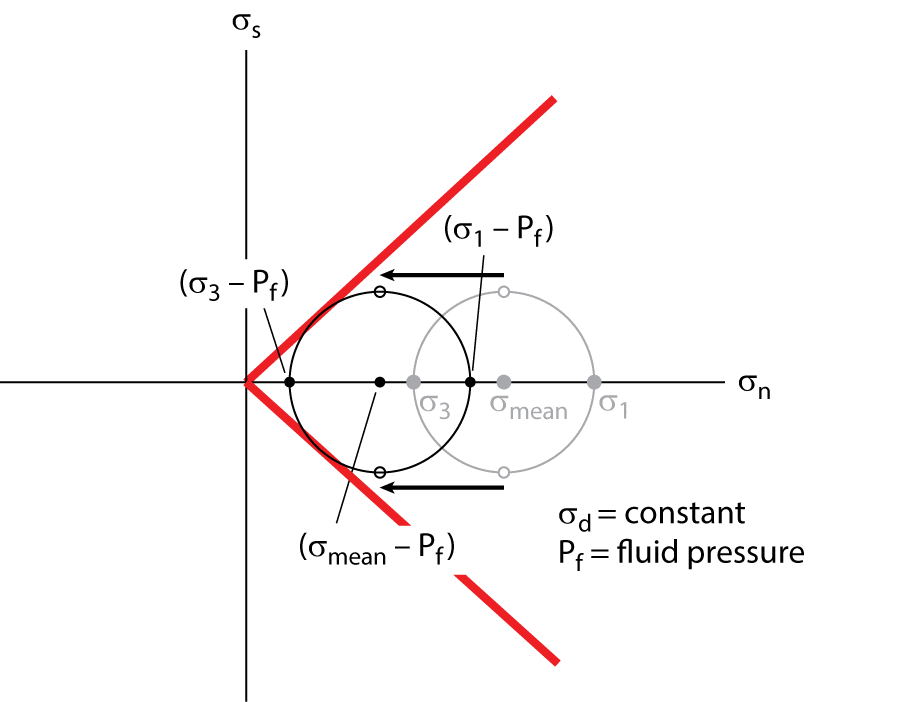 |
Figure 3.30. A Mohr construction showing how an increase in pore fluid pressure (Pf) moves the Mohr circle toward the friction envelope. The increase in fluid pressure decreases the mean stress (σmean), but does not change the magnitude of the differential stress (σd) nor the maximum shear stress (σs).
|
In a Mohr diagram we readily see the effect of increasing the Pf in this experiment (Figure 3.30). When Pf is increased, the whole Mohr circle moves to the left, but its diameter remains unchanged, and when the circle touches the failure envelope, shear failure occurs, even if the relative values of σ1 and σ3 are unchanged. In other words, a differential stress that is insufficient to break a dry rock, may break a wet rock, if the fluid in the wet rock is under sufficient pressure. Thus, an increase in pore pressure effectively weakens a rock. In the case of forming a shear fracture in intact rock, pore pressure plays a role by pushing open microcracks, which coalesce to form a rupture at smaller remote stresses. Similarly, an increase in pore pressure decreases the shear stress necessary to initiate frictional sliding on a preexisting fracture, for the pore pressure effectively decreases the normal stress across the fracture surface. Thus, as we discuss further in Chapters 4 and 5, fluids play an important role in controlling the conditions under which fractures and faults occur.
The limiting stresses derived above are similarly affected by fluid pressure, changing equation 3.8 to:
σd ≥ β (ρ ⋅ g ⋅ z) (1 – λ) Eq. 3.10
where σd is differential stress (i.e., 2σs) and λ is a fluid pressure parameter. This parameter is defined as the ratio of pore-fluid pressure and lithostatic pressure, with λ ranging from ∼0.4, for hydrostatic fluid pressure, to 1 for lithostatic fluid pressure.
Back to The Frictional Regime Contents