Ask a structural geologist, or any other geologist for that matter, about their favorite geologic structure and chances are that they will choose folds. If you have seen a fold in the field you will have marveled at its appearance (Figure 8.1). Let’s face it, it is pretty unbelievable that tough rocks are able to change shape in such a dramatic way. In simple terms, a fold is a structural feature that is formed when planar surfaces are bent or curved. If such surfaces (like bedding, cleavage, inclusions) are not available you will not see a fold even though the rock was deformed. Folding is a manifestation of ductile deformation because it can develop without fracturing, and the deformation is (heterogeneously) distributed over the entire structure. Rather than fracturing, processes such as grain sliding, kinking, dissolution, and crystal plasticity dominate. Looking at a fold from a kinematic perspective, you realize that strain in this structure cannot be the same everywhere. We recognize distinct segments in a fold, such as the hinge area and the limbs, the inner and the outer arc, each of which reflect different strain histories, regardless of scale.

FIGURE 8.1. North-verging recumbent fold in Mesozoic rocks of the Morcles thrust (Helvetic Alps, Switzerland). GE: 46°11'56" N 7°04'17" E [9.1]

Why do folds exist, how do rocks do it, and what does folding mean for regional analysis? These and other questions were first asked quite some time ago and much of what we know today about folds and folding was well established before the 1980s. The geometry of folds tells us something about, for example, the degree and orientation of strain, which in turn provides critical information about the deformation history of a region. Much of the work in recent years represents refinements of some of the earlier work; we can apply increasingly sophisticated numerical and experimental approaches. Yet, the fundamental observations remain essentially intact. Therefore, in this chapter we will mainly look at some of the first principles of folding and their application to structural analysis. First, however, we discuss the basic vocabulary needed to communicate about folds and fold systems.

ANATOMY OF A FOLD

FIGURE 8.2. The basic terminology of a fold. [10.2]

The schematic illustration in Figure 8.2 shows the basic geometric elements of a fold. The hinge area is the region of greatest curvature and separates the two limbs. The line of greatest curvature in a folded surface is called the hinge line. You may think of a limb as the less curved portion of a fold. In a limb there is a point where the sense of curvature changes, called the inflection point. Folds with a straight hinge line (Figure 8.3a) are called cylindrical folds when the folded surface can wrap partway around a cylinder. If this is not the case and the hinge line curves, the folds are called non-cylindrical (Figure 8.3b). In reality the lateral extent of cylindrical folds is restricted to the outcrop scale or even less, because over greater distances the hinge line of folds typically curves. Nevertheless you will find that we may conveniently treat natural folds as cylindrical by dividing them into segments with straight hinge lines.

FIGURE 8.3. A cylindrical fold (a) is characterized by a straight hinge line and a non-cylindrical fold (b) by a curved hinge line. The axial surface may be planar, as in (a) and (b), or curved (c). [10.3]

A cylindrical surface consists of an infinite number of lines that are parallel to a generator line. This generator line is called the fold axis, which, when moved parallel to itself through space, outlines the folded surface. In the case of cylindrical folds the fold axis is of course parallel to the hinge line [1]. The topographically highest and lowest points of a fold are called the crest and trough, respectively, and these do not necessarily coincide with hinge lines. The surface containing the hinge lines from consecutive folded surfaces in a fold is the axial surface (Figures 8.2 and 8.3). The term axial plane is loosely used by some, but the surface is not necessarily planar as seen in Figure 8.3c (recall the distinction between surface and plane). Moreover, the axial surface does not necessarily divide the fold into equal halves that are mirror images of one another.

The reference plane used to describe fold shape is called the fold profile plane, which is perpendicular to the hinge line (Figure 8.2). Note that the profile plane is not the same as a cross section through the fold, which is any vertical plane through a body, much like the sides of a slice of layered cake. If the hinge line is not horizontal, then the profile plane is not parallel to the cross-sectional plane, which has implication for the fold geometry description.

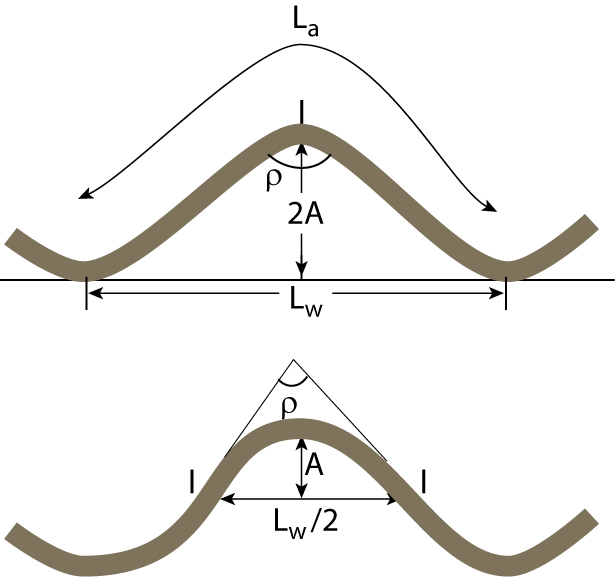
FIGURE 8.4. The interlimb angle (ρ), the wavelength (Lw), the amplitude (A), and the arc length (La) of a fold system in profile. [10.4]

The angle between fold limbs as measured in the profile plane is called the interlimb angle (Figure 8.4). Intuitively you realize that the interlimb angle offers a qualitative estimate of the intensity of folding; the smaller the interlimb angle, the greater the intensity of folding. Finally, we define the amplitude (A), wavelength (Lw), and arc length (La) of a fold in profile. These terms are used in the same manner as they are in wave physics, because folds tend to look like harmonic functions (such as a sine curve). The wavelength is defined as the distance between two hinges of the same orientation, while the arc length is this distance measured over the folded surface; the amplitude is half the height of the structure measured from crest to trough (Figure 10.4). These and other terms associated with folds are also summarized the Supplementary Material section.

FIGURE 8.5. Small-scale disharmonic folds in anhydrite of the Permian Castile Formation in the Delaware Basin of Texas. White layers are anhydrite; dark layers consist of calcite that is rich in organic material (hence dark color). Note that detachments occur in the organic-rich calcite layers and that the fold shapes (including box folds) in the anhydrite vary as a function of layer thickness. [10.5]

When successive layers in a folded stack have approximately the same wavelength and amplitude, the folds are called harmonic. If some layers have different wavelengths and/or amplitudes, the folds are disharmonic (Figure 8.5). In extreme circumstances, a series of folded layers may be totally decoupled from unfolded layers above or below. When this happens, a detachment horizon exists between folded and unfolded layers.

Fold Facing: Antiform, Synform, and Anticline, Syncline

Take a deep breath. We have already sprung a sizable array of terms on you, but before we explore the significance of folding, we have yet to add a few more. Maybe you will find comfort in the knowledge that generations of students before you have plowed their way through this terminology, happily discovering that in the end it really is important for the description and interpretation of regional deformation. Having said this, now draw a fold on a piece of paper. Chances are that you place the hinge area at the top of the structure, outlining something like a sharp mountain. In fact, a psychological study among geologists found this invariably to be true [2]. This particular fold geometry is called an antiform. The opposite geometry, when the hinge zone is at the bottom (outlining a valley), is called a synform. The explanation for the modifiers “anti” and “syn” is that the limbs dip away from or toward the center of the fold, respectively. You will find that many geologists use the terms anticline and syncline as synonyms for antiform and synform, but this is incorrect. The terms anticline and syncline imply that the stratigraphic younging direction in the folded beds is known. This is an important distinction for regional analysis, so let’s look at this in some detail.


FIGURE 8.6. Antiforms, synforms, and fold facing. An upward-facing antiform (a) is also called an anticline and an upward-facing synform (b) is called a syncline. Downward-facing antiforms (c) and downward-facing synforms reflect an early history that placed the beds upside down prior to folding. These forms may occur in a region containing two generations of folding (e). The corresponding facing in map view across this area is shown in (f). Younging direction is indicated by O→Y arrow. [10.6]

Imagine a sequence of beds that is laid down in a basin over a period of many millions of years. Obviously, the youngest bed lies at the top while the oldest bed is at the bottom of the pile (this is Steno’s Law of Superposition). When we fold this sequence into a series of antiforms and synforms, we see that the oldest bed lies in the core of the antiform and the youngest bed lies in the core of the synform (Figure 8.6a and 8.6b). Under these circumstances we call them anticlines and synclines, respectively. In an anticline the beds young away from the core; in a syncline the beds young toward the core. In both cases the younging direction points (or faces) upward, so we call these structures upward-facing folds. Now turn the original sequence upside down: the oldest bed now lies at the top and the youngest bed at the bottom (Figure 8.6c and 8.6d). While we generate the same geometry of antiforms and synforms, the younging direction is opposite to what we had before. In this antiform, the beds young toward the core, while in the synform the beds young away from the core. Both cases illustrated are downward-facing folds, and an antiform with this younging characteristic is therefore called a downward-facing antiform; analogously, we recognize a downward-facing synform. As they have the younging characteristics of a syncline and anticline, respectively, they are also called, gasp, antiformal syncline and synformal anticline, respectively.

When you find downward-facing folds in the field, you immediately know that some secondary process has inverted the normal stratigraphic sequence; that is, we cannot violate the Law of Superposition. Downward-facing folds are not as uncommon as one might guess. They are typically found in areas containing an early “generation” of regional folds with horizontal axial surfaces, which are quite common in collisional mountain belts. Subsequent folding of these early structures generates a series of upward- and downward-facing folds, as shown in Figure 10.6e. But we must not get ahead of ourselves; the principle of superposed folding is discussed in a later section of this chapter.

FOLD CLASSIFICATION

Now that we have established a basic vocabulary we can further classify folds. The classification of folds is based on four components:

Fold shape in three dimensions, primarily distinguishing between cylindrical folds and noncylindrical folds (Figure 8.3).
Fold facing, separating upward-facing folds and downward-facing folds (Figure 8.6).
Fold orientation.
Fold shape in the profile plane.

The first two components, three-dimensional fold shape and fold facing, have already been introduced. In this section we concentrate on the other two components of fold classification: fold orientation and fold shape.

Fold Orientation

Looking at the curved surface of a natural fold makes one wonder if there is any one representative measurement for the structure (Figure 8.7). Taking your compass to the folded surface will give you a large number of different readings for dip, and dip and strike (or dip direction) if the fold is noncylindrical. In folds with limbs that are relatively straight, you will find that all the measurements in a single limb are pretty much alike (Figure 8.8), but in folds with curving limbs this will not be the case.

FIGURE 8.7. An asymmetrical, plunging fold (the Sheep Mountain Anticline (Wyoming, USA). GE: 44°37'05" N 108°08'27" W ([10.7]

FIGURE 8.8. Chevron folds in Franciscan chert of California (Marin County, USA). [10.8]

So what do we measure if we want to give the orientation of a fold to another geologist? The first measurement we take is the orientation of the hinge line (Figure 8.9). On the scale of an outcrop the hinge line is typically fairly straight, and we determine its plunge (say, 20°) and direction of plunge (say, 190°). We now say that the fold is shallowly plunging to the South. Secondly, we measure the orientation of the axial surface. We measure a dip direction/dip of 270°/70° for the axial surface, which completes our description of the fold: a shallowly south-plunging, upright fold. Remember that the hinge line always lies in the axial surface. Test your measurements in a spherical projection to see whether this relationship holds.

FIGURE 8.9. Fold orientation. Note that the axial surface is a plane whose orientation is given by dip and strike (or dip direction), whereas the hinge is a line whose orientation is given by plunge and bearing. [10.9]

What constrains terms like shallow and upright? As a practical convention we use the angular ranges below for fold classification by orientation:

Plunge of Hinge Line Dip of Axial Surface

Horizontal: 0°–10° Recumbent: 0°–10°

Shallow: 10°–30° Inclined: 10°–70°

Intermediate: 30°–60° Upright: 70°–90°

Steep: 60°–80°

Vertical: 80°–90°

In Figure 8.10 we show some representative combinations of hinge line and axial surface orientations with their terminology. A fold with a horizontal axial surface by definition must have a horizontal hinge line, and is called a recumbent fold. In the European Alps, for example, large-scale recumbent folds are often associated with thrust faulting, and they are called nappes (Figure 8.1). A term that is used for a steeply plunging, inclined fold is a reclined fold. In all cases remember that your field measurements will be no more accurate than ±2° (compass accuracy), but that the feature you measure will probably vary over an even greater angle of ±5°–10°. Thus, the values in Table 10.2 serve as a guide and should not be applied too strictly; they are not carved in stone.

FIGURE 8.10. Fold classification based on the orientation of the hinge line (red) and the axial surface (shaded). [10.10]

Fold Shape in Profile

The profile plane of a fold is defined as the plane perpendicular to the hinge line (Figure 8.2). The fold shape in profile (as viewed, by convention, down the plunge) allows further classification of folds. Because the profile plane is perpendicular to the hinge line, we need not concern ourselves with the orientation of the fold. Fold shape in profile describes the interlimb angle and any changes in bed thickness. The interlimb angle of a fold is the angle between the limbs. We assume that the limbs are relatively planar or we use the tangent at the inflection points (Figure 10.4). The values corresponding to the various terms are:

Isoclinal 0°–10°

Tight 10°–60°

Open 60°–120°

Gentle120°–180°

As with other such numbers, they serve as a rough guide to describe fold classification by interlimb angle.

The second characteristic of fold shape in profile is any change in bed thickness across the structure. If you look at Figure 8.11a, you will notice that the bed thickness does not change appreciably as we go from one limb of the fold to the other. In contrast, the fold in Figure 8.11b has thin limbs and a relatively thick hinge area. The two geometries shown in Figure 8.11 are end-member cases, called parallel fold and similar fold, respectively. This terminology (especially the use of “parallel”) may be confusing, but remember that parallel and similar describe the geometric relationship between the top and bottom surfaces of a folded layer. Another method to describe fold shape, called dip isogon analysis, is presented in Supplementary Material, which also formalizes the parallel and similar fold type categories.

FIGURE 8.11 Parallel folds (a) maintain a constant layer thickness across the folded surface, meaning, t1 = t2 = t3, but the layer thickness parallel to the axial surface varies (T1 < T2 < T3). Note that parallelism must eventually break down in the cores of folds because of space limitation, illustrated by the small disharmonic folds in (a). In similar folds (b), the layer thickness parallel to the axial surface remains constant, so, T1 = T2 = T3, but the thickness across the folded surface varies (t1 > t2 > t3). Similar folds do not have the space problem inherent in parallel folds. [10.11]

So, we added two more components to our description of a fold. Now as a test, sketch a shallowly plunging, upright, tight, similar, downward-facing synform in the margin of the text. Hopefully these terms have become sufficiently clear that the task, unlike its description, is relatively simple. The only parameter we have excluded in our classification is fold size. To specify this we can use terms like micro-fold (microscopic size; up to millimeter scale), meso-fold (hand specimen to small outcrop size; centimeter to meter scale), and macro-fold (mountain size and larger; hundreds to thousands of meters). Although the lengthy description above is certainly not pretty, it ends up being very informative and complete. Remember that the goal of any good description is first to recall the characteristics for yourself, and secondly to relay this information in an understandable and unequivocal fashion to someone else.

FOLD SYSTEMS

Our treatment of folds so far has concentrated mostly on single antiforms and synforms. When we have a series of antiforms and synforms, we call this a fold system. The information we can obtain from fold systems provides some of the most powerful information for the interpretation of regional structure, and involves such elements as fold symmetry, fold vergence, and the enveloping surface. We start with the last of these.

The Enveloping Surface

Draw an imaginary plane that is tangential to the hinge zones of a series of small folds in a layer (surface A, Figure 8.13). We call this surface the enveloping surface. It contains all the antiformal or synformal hinges. In the case of folds with horizontal or shallowly dipping axial surfaces, we refer to these as crests and troughs, respectively. Figure 8.13 also shows that we can draw an additional enveloping surface (surface B) when we connect the hinges of the curved enveloping surface A. We call the enveloping surface for the largest folds the first-order enveloping surface (here surface B). The enveloping surfaces of successively smaller structures have a higher order (second-order enveloping surface, third order enveloping surface, and so on).

FIGURE 8.13 The enveloping surface connects the antiform (or synform) hinges of consecutive folds (surface A). If this imaginary surface appears to be folded itself, we may construct yet a higher-order enveloping surface (surface B). Note that the orientations (hinge line and axial surface) of the small folds and the large-scale folds are very similar. [10.13]

The first-order enveloping surface is typically of regional scale, while higher-order enveloping surfaces may go down as low as the thin-section scale. But what is the point of determining the enveloping surface? With decreasing order, the enveloping surfaces reduce the structural information of a folded area into increasingly simple patterns. For example, the second-order enveloping surface in Figure 8.13 shows that the small-scale folds define a larger-scale fold pattern consisting of antiforms and synforms. These large-scale structures have also been designated by the terms anticlinorium and synclinorium, respectively. Unfortunately the use of these terms suggests upward-facing structures, which is not always intended. The presence of anticlinoria and synclinoria implies that many small folds are somehow related, even though they vary in shape and position in the larger structure. It is important to realize that the orientations of these small folds (both hinge line and axial surface) are often the same, and also that these parameters approximately parallel that of the anticlinorium and synclinorium. For that reason, these small folds are sometimes called parasitic folds, because they are related to a larger structure.

The geometric relationship between parasitic folds and regional structures offers a powerful concept in structural analysis, which states that the orientation of small (high-order) structures is representative of the orientation of regional (low-order) structures. Thus, the orientations of the hinge line and the axial surface of a small fold can predict these elements for a large regional fold that is otherwise not exposed; in Figure 8.13 you indeed see that this is the case. Obviously, this “rule” serves only as a convenient working hypothesis, but it has proven to be very robust in regional mapping. Use this rule on a field trip and surprise friend and foe with your quick insight into regional structure.

Fold Symmetry and Fold Vergence

The relationship between the enveloping surface and the axial surface of folds also enables us to describe the symmetry of folds. If the enveloping surface and the axial surface are approximately perpendicular (±10°), we have symmetric folds (Figure 8.14a); otherwise the folds are asymmetric (Figure 8.14b). In the case of an isolated fold, an enveloping surface cannot be defined.

FIGURE 8.14. Symmetric (a) and asymmetric folds

(b) are defined by the angular relationship between the axial surface and the enveloping surface. [10.14]

To determine if a fold is symmetric or asymmetric we use the median surface, which is the surface that passes through the inflection points of opposing limbs. If the axial surface is perpendicular to the median surface, then the fold is symmetric; otherwise the fold is asymmetric. There are other definitions of fold symmetry that involve, for example, the relative steepness of limbs, but these descriptions of fold symmetry are often ambiguous and should not be used.

Now let’s look at a practical application of fold symmetry. The second-order enveloping surface defined by the small folds of Figure 8.13 outlines a large antiform-synform pair. The small folds (the parasitic folds) show characteristic shapes and asymmetries as we move along the second-order enveloping surface. On the west limb of the large antiform, the minor folds are asymmetric and have what we call a clockwise asymmetry when looking down the plunge of the fold. In the hinge area, the folds are symmetrical, because the axial surface is perpendicular to the enveloping surface. In fact, as we move from the limb toward the hinge area, the clockwise asymmetry becomes progressively less, until the fold is symmetrical. As we move into the east limb of the antiform, the fold asymmetry returns, but now with the opposite sense to that in the west limb; in the east limb the asymmetry is counterclockwise.

FIGURE 8.15. Fold vergence, clockwise (a) and counterclockwise (b), is defined by the apparent rotation of the axial surface from a hypothetical symmetric fold into the observed asymmetric fold, without changing the orientation of the enveloping surface. In a given geographic coordinate system we may also say east-verging (a) and west-verging (b) folds for clockwise and counterclockwise folds, respectively (for this example). In all descriptions we are looking down the plunge of the fold. [10.15]

In this definition, clockwise and counterclockwise are defined by the rotation of the axial surface relative to a hypothetical symmetrical fold (Figure 8.15). In the past, parasitic folds were erroneously given the genetic name “drag folds,” because it was assumed that the apparent rotation of the axial surfaces reflects drag between the layers during folding. Rather, these minor folds are probably symmetrical in the incipient stages of regional folding and become more asymmetrical when the large folds tighten. So, across a large fold the vergence of parasitic folds changes in a characteristic manner that allows us to predict the location of the hinge area of large antiforms and synforms (Figure 8.16). Using parasitic folds, we may even predict the orientation of large regional folds (see previous section). But do not confuse fold vergence with fold facing.

FIGURE 8.16 (a) Characteristic fold vergence of parasitic folds across a large-scale antiform. Looking down the plunge, the parasitic fold changes from clockwise asymmetry (east verging in the geographic coordinate system) to symmetric to counterclockwise asymmetry (west-verging) when going from W to E. You may also find that some geologists use the terms Z-, M-, and S-folds for this progression. (b) Right and wrong in fold vergence. It is useful to copy these images in your field notebook for future reference. [10.16]

There is need for some caution when folds are not plunging; that is, in horizontal upright folds where down-plunge observations cannot be made. If we view the structure in Figure 8.16 from the opposite side, the clockwise folds become counterclockwise (just hold the page with Figure 8.16 facing the light, viewing it from the back)! This situation is not as confusing as it seems at first. Imagine an antiform that is cut by a road perpendicular to the axial surface. The asymmetry of parasitic folds in this large structure appears clockwise or counterclockwise on opposite sides of the road. However, in both cases they make the same prediction for the location of the hinge area. As long as you define the direction in which you view the minor structure, there is no problem using fold vergence as a mapping tool in an area. A practical tip is to copy the geometry of Figure 10.16 into the back of your field notebook. Matching field observation with asymmetries in your sketch, which may require some rotation of your notebook, will ensure a reliable application of this mapping tool. In any case, remember that a pattern of fold vergence opposite to that in Figure 8.16 (a “Christmas-tree” geometry) cannot be produced in a single fold generation.

A FEW SPECIAL FOLD GEOMETRIES

We end the descriptive part of this chapter by taking a look at a few characteristic fold geometries that you will likely encounter in your field work.

FIGURE 8.18. (a) Monocline in the Big Horn Mountains (Wyoming, USA), and (b) Kink folds in mica-rich portion of greywackes of the Cantabrian Mountains (northern Spain). [10.18]

Monoclines are fold structures with only one tilted limb; the beds on either side of the tilted limb are horizontal. Monoclines typically result from a vertical offset in the subsurface near the tilted portion of the structure. The fault uplifts a block of relatively rigid igneous or metamorphic rock, and the overlying sedimentary layers drape over the edge of the uplifted block to form the monocline (Figure 8.18a). Spectacular examples are found in the Colorado Plateau of the western United States.

Kink folds are small folds (less than a meter) that are characterized by straight limbs and sharp hinges. Typically they occur in finely laminated (that is, strongly anisotropic) rocks, such as shales and slates (Figure 8.18b). Sharply bending a deck of cards is a good analogy for the kinking process, because kink folds are formed by displacements between individual laminae (individual cards in the analogy). Chevron folds (Figure 8.8) are the larger-scale equivalent of kink folds.

FIGURE 8.19. Ptygmatic folds in the Grenville Supergroup (Ontario, Canada); hammer for scale. Notice the wavelength variation as a function of layer thickness. [10.20]

The term box fold describes a geometry that is pretty self-explanatory (Figure 8.5). In order for a box fold to form, a layer must be detached from the underlying and overlying layers. They are therefore common in areas with weak basal layers, such as in the Jura Mountains of Switzerland. Ptygmatic folds are irregular and isolated fold structures that typically occur as tightly folded veins or thin layers of strongly contrasting lithology (and, thus, contrasting competency; Figure 8.19). Most metamorphic regions around the world contain ptygmatic folds, which, unglamorously, resemble intestines.

FIGURE 8.20. (a) En echelon folds on the scale of a hand specimen (Spain); coin for scale. [10.21]

Doubly plunging folds are structures with hinge lines that laterally change curvature. Along the trend of plunge the folds may die out or even change from antiforms to synforms. The high point of the hinge line in a doubly plunging fold is called the culmination and the low point along the same hinge line is called a depression. The change in plunge angle is normally less than 50°. When additional folds are present, changes in plunge may result in en echelon folds, in which a gradually opening fold is replaced by a neighboring, gradually tightening fold of opposite form. Such a geometry occurs on all scales, from hand specimens (Figure 8.20) to the size of mountain ranges (such as the Valley-and-Ridge of the central Appalachians, eastern USA). Note that doubly plunging folds are, by definition, non-cylindrical.

MECHANICS OF FOLDING

Why does folding occur? After spending most time on the description of folds and fold systems so far, this is a question whose time has come. Well, if you ever saw a car collision you do not need to be reminded that forces can cause folding [3]. Indeed, forces applied to rocks cause folding, but we will see that forces alone are not sufficient to form folds. Consider a block of clay that is reshaped by external forces (from your hands). The block will change form, but in doing so the internal structure does not show any folds (Figure 8.21a).

FIGURE 8.21. Compression of (a) a clay block of uniform color, (b) with irregularly shaped layers of different colors, or (c) with uniform colored layers separated by thin sheets of rubber. [10.27]

After we add irregularly shaped layers of different color but with the same material properties to the block, we get folds when the irregularities are amplified (Figure 8.21b). If we add straight, thin sheets of rubber to our clay block and a force is applied, folds also appear (Figure 8.21c). These experiments provide us with a fundamental subdivision of folding based on the mechanical role of layers: passive folding and active folding.

Passive Folding and Active Folding

During passive folding the layering of a material has no mechanical significance. In the color-banded clay block, folds are formed by the amplification of small perturbations in the bands, but the strain pattern in the block is unaffected by the presence of these layers. Squeezing multicolor toothpaste on a counter top is a fresh and minty experiment where complex folding patterns are visible only because of the color contrast; if you do the same experiment with single-color toothpaste you will not see folds, even though the internal structure of the two blobs is similar. We find such toothpaste-like behavior in nature where rocks have little or no competency contrast between layers. Elevated temperatures can produce the right conditions for passive folding and it is common to find toothpaste-like structures in deformed metamorphic rocks. Rocks that were deformed at or near their melting temperature (that is, a high homologous temperature, Th = T/Tm) are called migmatites, which often contain wonderfully complex fold structures (see Chapter 1). Similarly, passive folding occurs in glaciers that deform close to their melting temperature. Passive folds are the amplification of natural irregularities in the layers, or are a consequence of differential flow in a volume of rock. But don’t think that passive folds have to be chaotic in appearance because of this. Sheath folds in a shear zone are another natural example of passive folding and typically show very consistent orientation and style.

Figure 8.22. Bending (a) and buckling (b) of a layer. [10.28]

During active folding, layering has mechanical significance. This means that the presence of layers with different competency directly affects the strain pattern in the deforming body and that there is contrasting behavior between layers. There are two dynamic conditions that we distinguish for active folding: bending and buckling. In bending, the applied force is oriented at an oblique angle to the layering (Figure 8.22a). In nature this may occur during basin formation or loading of a lithospheric plate (also called flexural loading), or during the development of monoclines over fault blocks. In buckling, the force is oriented parallel to the mechanical anisotropy (Figure 8.22b), the most common situation for folding, which we’ll explore further below.

Buckle Folds

FIGURE 8.23. Classroom deformation experiments with transparent boxes containing foam and rubber bands. In (a), four starting settings are shown that contain, from left to right, foam only (with marker line added), a thin, a medium, and a thick rubber band. When applying the same displacement (b), the setups respond differently. The foam-only box shows thickening of the marker line, but no folding. The boxes with rubber bands show folds with arc lengths varying as a function of thickness of each band. When using more than one band (c), the behavior depends on the combination of bands and their thicknesses, with the effect of the thicker bands dominant. [10.29]

Let’s see what happens in a series of analog experiments of folding (Figure 8.23). We surround a band of rubber with foam in a plastic box that is open at one end, at which we place a plunger. As we push on the plunger, the band of rubber forms a series of folds. The surrounding foam (the “matrix”) accommodates the shape of the rubber band by filling the gaps that would otherwise be present. We repeat the experiment with a thinner band of rubber and the same foam. Now we produce several more folds and the weaker foam again accommodates this new pattern. So, in spite of applying the same force and producing the same bulk shortening strain, the folding patterns are different as a function of the thickness of the rubber band. In other words, the rubber band introduces a mechanical anisotropy.

We return to the above rubber band–foam experiments, where we saw that the thickness of the band somehow affects the fold shape, to explore some systematic properties of buckle folds. The applied force (and thus stress), the bulk strain (the distance the plunger moves into our box), the strain rate (the speed at which the plunger moves), and the ambient conditions (room temperature and pressure) are assumed to be the same in all experiments; only thickness, t, of the layer varies. We notice that with increasing thickness the wavelength and arc length become larger. Secondly, if we use bands of equal thickness but with different stiffness, we find that arc length of the stiffer layer is larger than that of the weaker layer. So, we find that both thickness and the parameter “stiffness” increase the wavelength. Folds are not deformed elastic layers; they are permanent strain features. Therefore, we examine them in terms of linear viscous behavior or more complex rheologies (such as elastico-viscous or nonlinear viscosity; see Chapter X). For our current purposes in this chapter we focus on Newtonian (linear) viscous behavior.

Using Newtonian viscosity, the theoretical wavelength–thickness relationship for a layer with viscosity ηL surrounded by a matrix with viscosity ηM is:

LW = 2π t (ηL/6ηM)1/3 Eq. 8.1

This equation, known as the Biot- Ramberg equation [4], tells us that wavelength is directly proportional to thickness and to the cube root of the viscosity ratio. Therefore, if we know the wavelength/thickness ratio of a layer, we can obtain the viscosity ratio. Reorganizing Equation 8.1, we get:

ηL/ηM = 0.024 (LW/t)3 Eq. 8.2

This formulation states that the viscosity ratio is proportional to the cube of the LW/t ratio. For example, the measurements of folded sandstone layers in sedimentary rocks of the Appalachians, shown in Figure 8.24, give a viscosity ratio of about 500.


FIGURE 8.24. (a) The oft-visited Sideling Hill syncline of the US Appalachians (Maryland). (b) Log–log plot of wavelength versus layer thickness in folded sandstone layers across a range of thicknesses. [10.30]

We intentionally say “about,” because Figure 8.24b is a log–log plot, meaning that a small change in LW/t ratio will result in a large change in viscosity ratio. Try the same analysis for our box experiments above toward producing a viscosity ratio between foam and rubber. You’ll find that these analog experiments offer a reasonable approximation of the mechanical properties of low-grade sandstone-shale deformation.

There is an additional consequence when the viscosity ratio of layer and matrix is small (say, <<100). Again we return to our box experiments. This time we place only foam in our plastic box. On the foam we draw a vertical line with a marker pen (Figure 8.23) to represent a layer with a small viscosity ratio (in this case, of course, ηL/ηM = 1). As we compress the foam we do not get any folds, but we find that the layer thickens. So, low viscosity contrasts result in a pronounced component of strain-induced layer thickening, which we describe in Supplementary Materials.

Our examination of folding is entirely based on Newtonian or linear-viscous behavior of both the layer and the matrix. However, it is likely that folding under elevated conditions of pressure and temperature involves nonlinear rheologies, in which the viscosity is stress dependent (Chapter 10). Without going into any details, we only mention that appropriate nonlinear rheologies result in lower values of LW/t as well as small to negligible components of layer-parallel shortening. Natural folds in metamorphic terrains typically have low LW/t ratios (< 10), suggesting that nonlinear viscous rheology and crystal- plastic processes, are more important for folding under these conditions.

Folded Multi-layers

Our discussion so far has focused on folding of a single layer in a weaker matrix. While this situation occurs in nature, it is not representative. What happens when several layers are present? Again we turn to our simple experimental setup (Figure 10.29), but now use two rubber bands of equal thickness to see what folds develop. Can you explain why the results differ from those of our previous single-layer experiments? The wavelength in the multilayer experiment is greater and the two layers seem to act as a thicker single layer. In another experiment we combine a thick and a thin layer (Figure 10.29). In this case, the thin layer does not at all give the fold shape predicted from single-layer theory, while the thick layer behaves pretty much the same as predicted from the single-layer experiment. In fact, the thin layer mimics the shape of the thick layer, indicating that its behavior is dominated by that of the thick layer.

We can try many other combinations, which all show that the behavior of a multi-layer system is sensitive to the interaction between layers. The previous Biot-Ramberg buckling theory, therefore, only applies when layers in natural rocks are sufficiently far removed from one another to avoid interaction. We can theoretically determine the region over which the effect of a buckled layer in a weaker matrix dies off to negligible values. This is known as the contact strain zone (CSZ). The width of this contact strain zone (2dCSZ, where dCSZ is the distance measured from the midpoint of the buckled layer) is a function of the arc length:

dCSZ = 2/πLW Eq. 8.4

Practically this means that the width of the CSZ is slightly greater than the arc length of a fold, which seems supported by field observations on natural folds.

Interacting layers require only a slight extension of the theory, if we assume that a stack of several superposed thin layers are free to move relative to one another (that is, no coupling). The corresponding equation for this multilayer case is:

LW = 2π t (NηL/6ηM)1/3 Eq. 8.5

where LW is the wavelength of the multilayer, N is the number of layers, and the space between the layers is infinitely small. Note that this is not the same as the equation for a single layer with the same thickness (N⋅t). If we calculate the ratio of the wavelength of a system with N superposed multi-layers (LW(multi)) and a system with a single layer of thickness N.t (LW(single)), by dividing Eq. 8.1 and Eq. 8.5, we get:

LW(single)/LW(multi) = N2/3 Eq. 10.6

This shows that the arc length of N multilayers of thickness t is less than that of a single layer with thickness N.t. This scenario is certainly not applicable to all geologic conditions. Commonly we find that layers of one viscosity alternate with layers of another viscosity. For example, a turbidite sequence contains alternating layers of sandstone and shale. In this case the analysis is considerably more complex and, because increasingly restrictive assumptions have to be made (such as the spacing between layers), we end here. The key point is that multi-layers behave much like a thick single layer, but the resulting wavelength in a multilayer system will be somewhat less than that of a single layer.

KINEMATICS OF FOLDING

The distinction we made earlier between active and passive folds describes the mechanical role of layers under an imposed stress, but this says little about the inner workings of the folded layer and the associated strain pattern. To this end, we examine two end-member models, flexural folding and neutral-surface folding, and their modification by superimposed strain; each of them have distinct properties and characteristics. These models are compared with natural examples in the final section.

Flexural Slip/Flow Folding

Take a paperback or a deck of computer or playing cards, and bend it into a fold. The ability to produce the fold is achieved by slip on the surfaces of the cards relative to one another, without appreciable distortion within the surface of any individual card (they remain of the same size). If we place small marker circles on the top surface as well as on the sides of the card stack for use as a strain gauge, we see that strain only accumulates in surfaces that are at an angle to the individual cards (that is, the sides) when we fold the deck. The circles become ellipses in the profile plane (Figure 8.25) and on the other side of the folded deck parallel to the hinge line. Within the plane of each card, however, there is no strain, as seen from the fact that the circles on the top card in the deck remain circles.

FIGURE 8.25. The strain pattern of flexural folding in the fold profile plane (the plane perpendicular to the hinge line). [10.32]

Folds that form from slip between layers are called flexural slip folds. The amount of slip between the layers increases away from the hinge zone and reaches a maximum at the inflection point. Moreover, the amount of slip is proportional to limb dip: slip increases with increasing dip. The card deck analogy highlights three important characteristics of flexural slip folding. First, at each point in the profile plane the strain ratio and orientation differ. Second, in three dimensions the strain state of the fold is plane strain (X > Y = 1 > Z), with the orientation of the intermediate strain axis (Y) parallel to the hinge line. Third, a geometric consequence of the flexural slip model is that the fold is cylindrical and parallel (Class 1B); the bed thickness in flexural slip folds does not change. The geometric consequences of flexural slip folding are not diagnostic of the model, because they also occur in other models (see neutral-surface folding below). The strain pattern, on the other hand, is. Chevron folds (Figure 8.8) and kink folds (Figure 8.19) are examples of flexural slip folds in natural rocks that form because of a strong layer anisotropy.

Slip that occurs on individual grains within a layer, without the presence of visible slip surfaces, we call flexural flow folding. Although they differ in a few details, the geometric and kinematic consequences of both flexural slip and flexural flow folding are alike. A diagnostic feature of flexural slip folding that can be used in field analysis is that any original angular relationship in the slip surface before folding (say, flute casts in the bedding surfaces of turbidites) will maintain this angular relationship across the fold, because there is no strain on the top and bottom of the folded surface. Consequently, a lineation at an angle to the hinge line will distribute as a cone around the hinge line with that angle (a small-circle pattern in spherical projection).

Neutral-surface Folding

When we bend a layer of clay or a metal bar we obtain a fold geometry that seems identical to one produced by flexural folding, but with a distinctly different strain pattern. This is illustrated by tracking the distortion of circles drawn on the sides of the undeformed layer (Figure 8.26). On all three surfaces we find that circles have become ellipses, including the folded top and bottom surface. On the top folded surface, the long axis of each ellipse is perpendicular to the hinge line, but on the bottom the long axis is parallel to the hinge line. In the profile plane the long axis is parallel or perpendicular to the top and bottom surfaces of the folded layer, depending on where we are in that plane.

FIGURE 8.26. The strain pattern of neutral-surface folding as preserved in the fold profile plane. [10.33]

There must, therefore, be a surface in the fold where there is no strain. This zero-strain surface gives the model its name, neutral-surface fold. Trying to mimic this behavior with the deck of cards used earlier will require some muscle power, because the cards in the outer arc need to stretch while those in the inner arc are compressed.

The resulting fold shape from neutral-surface folding is parallel and cylindrical, with the intermediate bulk strain axis parallel to the fold axis. These geometric characteristics and plane strain conditions also hold for flexural slip folding, so they are not diagnostic for either model; their strain patterns, however, are. Because strain accumulates in the folded surfaces during neutral-surface folding, the orientation of any feature on these surfaces changes with position in the fold. In the outer arc an initial angle with the hinge line increases, while in the inner arc this angle decreases. So, the angle of flute marks with the hinge line on the top surface of the folded layer increases, while on the bottom surface this angle decreases. In both cases the orientations in any individual surface describe neither a cone nor a plane (or small circle and great circle in spherical projection, respectively). Only in the neutral surface is the angle unchanged and does the linear feature describe a cone around the hinge line. It is not easy to use this criterion as a field tool unless one measures lineations from individual top and bottom layers in a fold.

The strain pattern in the profile plane is characteristic, and is sometimes (cumbersomely) called tangential longitudinal strain. Note that the position of the neutral surface is not restricted to the middle of the fold, nor does it necessarily occur at the same relative position across the fold. In extreme cases the neutral surface may coincide with the outer arc, in which case the long axis of each strain ellipse in the profile plane is perpendicular to the folded surface. Is it possible to have the neutral surface at the inner arc? Try to answer this question to test your understanding of neutral-surface folding.

Fold Shape Modification

Whereas both flexural folding and neutral-surface folding produce parallel folds, similar folds are very common in nature, especially at increasing depth in Earth. This can be addressed by what happens when we allow modification of fold shape? Experiments and geometric arguments place a limit on the degree of strain that can be accumulated by fold tightening in parallel folds. You may have noticed this when folding the card deck, where the inner arc region increasingly experiences space problems as the fold tightens (Figure 8.11a). Material that occupies the inner arc region may be able to accommodate this space crunch, much like the foam does in our box experiments. However, as the fold tightens, the later strain increments will increasingly affect the entire fold structure (limbs and hinge equally), resulting in superimposed homogeneous strain. This strain component has a pronounced effect on the fold shape.

FIGURE 8.27. The effect of superimposed homogeneous

strain on (a) a flexural and (b) a neutral-surface fold. Constant

volume, plane strain with X/Z = 1.6 (20% shortening), and

X/Z = 6.3 (60% shortening) are shown. [10.35]

Figure 8.27 shows the effect of superimposed homogeneous strains (constant volume, plain strain) with 20% shortening (X/Z = 1.6) and 60% shortening (X/Z = 6.3) on shape and corresponding strain distributions in a flexural fold and a neutral-surface fold. You see that initially parallel folds change shape by thinning of the limbs relative to the hinge area, generating the geometry of similar folds.

Example Scenarios

How well does all this theory apply to nature? To answer this, we look at an example of a fold in a limestone-pebble conglomerate. Strain values that were measured from pebbles across the folded layer give an estimate of the overall strain pattern (Figure 8.28a). When comparing this pattern with those predicted for flexural folding (Figure 8.28c) and neutral-surface folding (Figure 8.28d), we see that the natural pattern most resembles that predicted by neutral-surface folding. The x-axis is parallel to the folded surface in the outer arc and perpendicular to this surface in the inner arc. Yet the magnitude of the strain ratios predicted by neutral-surface folding is too low in the natural pattern, so the pattern requires additional modification to match the natural fold. One solution is shown in Figure 8.28b, where prefolding compaction (non-constant volume, layer-perpendicular shortening) is followed by neutral- surface folding, during which material is preferentially removed from the inner arc. The example in Figure 8.28 shows that strain in folds is heterogeneous, but we can nonetheless estimate the bulk shortening strain from the fold shape by adapting the equation for the elongation (Equation 6.1). The bulk strain is given by e = (LW – LA)/LA, where LA is the arc length and LW is the wavelength. Applying this to our example we obtain a value for e of approximately –0.35, or ∼35% bulk shortening strain.

FIGURE 8.28. Strain pattern in a natural fold of limestone-pebble conglomerate (a). The pattern better resembles the strain predicted from neutral-surface folding (d) than from flexural folding (c). With further modification, which consists of initial compaction and material transport away from the inner arc region, a strain pattern much like that observed in the natural sample is produced (b). [10.37]

Dissolution and material transport during folding are quite common in natural rocks. Quartz and calcite veins in folded rocks are examples of this transport. Other natural folds show that flexural folding and shear folding are the dominant mechanisms, so all our folding models offer reasonable first-order approximations to the inner workings of a folded layer.

We close this section on fold kinematics with an example sequence of events in the formation of a single-layer fold (Figure 8.29).

FIGURE 8.29. Folding scenario with the corresponding strain states at each step. An initial layer (a) undergoes 20% compaction (b). This is followed by layer-parallel shortening (c) and buckling (d). The final stage is a homogeneous shortening strain which transforms the parallel fold into a similar fold. The finite strain in the layer is indicated at each step; the incremental strain (dashed) and finite strain (solid) ellipses of the system are shown in the upper right. Strain ratios are shown for each step. It is assumed that volume loss occurs only at the compaction stage (b). [10.38]

Immediately following deposition of the bed, compaction (denoted by sub-c) reduces its thickness. We use an intermediate value of 20% layer-perpendicular shortening strain for this first component in our example (i.e., Xc/Zc = 1.25), which represents 20% area loss (Figure 8.29b); in nature, compactional strains range from 0% to 50%. During the first stage of buckling, the competent layer changes dimensions by layer-parallel shortening (lps). You recall that layer thickening is more important at low viscosity ratios, so in our example we assume 20% layer-parallel shortening. This constant-volume, homogeneous strain component (conveniently) restores the finite strain ellipse to a circle (Xf/Zf = 1), but the corresponding lps strain ratio Xlps/Zlps is 1.25 (Figure 8.29c). Continued shortening results in the initiation and growth of a parallel fold by flexural folding, with a characteristic wavelength (LW)as a function of the thickness (t) of the layer and the linear viscosity ratio (ηL/ηM). We can estimate the viscosity ratio of the system by measuring the ratio LW/t and the strain ratio Xlps/Zlps of the layer. Until this buckling stage, the strain has been homogeneous, but after fold initiation the strain is heterogeneous, with coaxial strain dominating the hinge area and non-coaxial strain dominating in the limbs of the fold (Figure 8.29d). The finite strain of the system is represented by the ratio Xf/Zf (i.e., 4). When resistance to further folding has been reached, continued shortening is achieved by superimposed homogeneous strain (Figure 10.38e). The end result of these stages produces a similar fold with a strain pattern that varies as a function of the degree of compactional strain, the operative fold mechanism, the viscosity ratio, and the degree of superimposed homogeneous strain. The finite strain ratio Xf/Zf for this fold’s history is 11, which corresponds to a total layer-parallel shortening strain of ∼70%.

One can vary this scenario in many ways by simply changing the values of the strain ratio at each step, but also by introducing volume loss during the stages of buckling and superimposed homogeneous strain. Examining alternative scenarios will give you a good idea of folding and strain distributions under different conditions; modern imaging programs for personal computers offer a simple way to experiment. For example, in metamorphic rocks there is little competency contrast between the layers, and layer-parallel thickening may be much more important than in low-grade sedimentary beds. Moreover, elevated temperature conditions promote grain dissolution and transport of material. It is therefore particularly instructive to examine the history of a system experiencing 50% volume loss (Δ = –0.5) during the buckling and superimposed homogeneous strain stages. This represents a geologically reasonable condition we will return to in the chapter on Fabrics (Chapter 9).

FAULT-RELATED FOLD GEOMETRIES

Geologists refer to field areas like the Canadian Rockies and the Appalachian Valley and Ridge Province as fold-thrust belts because, in addition to the thrusts that we earlier described, these regions contain spectacular folds, with amplitudes ranging from millimeters up to a few kilometers. We call these folds “fault-related folds” because they form in association with displacement on faults, especially in thrust systems. We recognize three main categories, based on the specific relationship between a fold and the underlying fault.

Fault-bend Folds

Picture a simple thrust geometry in which a thrust that occurs as a flat in a weak layer bends, cuts up section across a strong layer as a ramp, and then bends again and becomes a flat at the top of the strong layer (Figure 8.30).

FIGURE 8.30. (a) Cross-sectional model showing the progressive stages during the development of a fault-bend fold. The dashed lines are the traces of axial surfaces. [18.18]

[Animation]

If you push on the thrust sheet, the sheet must itself bend to climb the ramp. Because of Earth’s gravity, the sheet cannot rise into the air at the top of the ramp. Rather, the layer bends again to form an anticline on the upper flat. Thus, by pushing strata up and over a preexisting stair-step thrust, strata of the thrust sheet must undergo folding (Figure 8.31). Note that this folding occurs after the formation of the thrust. The resulting fold is called a fault-bend fold. In sum, a fault-bend fold forms where hangingwall strata move up and over a stair-step in a fault; the strata deform in order to conform to changes in dip (bends) of the fault surface.

FIGURE 8.31. Photo of a fault-bend fold over a ramp in the McConnell Thrust (Mt Yamnuska, Alberta, Canada). These Paleozoic strata have been displaced over 5 km vertically and 40 km horizontally, and now lie above Cretaceous foreland basin deposits. The foreland basin deposits have preferentially eroded and are now forested. (shown as mirror image)

The geometry of a specific fault-bend fold depends on the geometry of the stair-step thrust beneath it. Note that if the bends in the fault surface are abrupt, the fold will have kink-style (i.e., not rounded) hinges. Also, note that once the fold has climbed over the ramp, the width of the anticline depends on the magnitude of displacement on the fault; as displacement increases, interlimb distance increases because the back limb (the limb closer to the hinterland) remains over the ramp. In an ideal fault-bend anticline, the fold’s backlimb parallels the footwall ramp, the fold’s forelimb is shorter and steeper than the backlimb, strata of the footwall remain flat-lying, and the kink-style hinges of the hanging-wall anticline directly reflect the shape of bends in the fault surface. In some cases, strata move through the kink hinges as the fold evolves.

Fault-propagation Folds

In some cases, folding develops just in advance of the tip of a ramp as the ramp propagates up dip. The resulting fold is called a fault-propagation fold.

Figure 8.32 Exposure of a fault-propagation fold in the Lost River Range, Idaho, showing an asymmetric fold dying out up dip, away from the fault tip.

Such folds develop concurrently with thrust development. Typically, a fault-propagation fold develops only in front of the upper tip line as the ramp propagates up section toward the ground surface. Fault-propagation folds are asymmetric and verge in the direction of thrusting (Figure 8.33). Displacement along the fault dies out in the hinge zone of the fold.

FIGURE 8.33. (a) Model for the development of a fault-propagation fold. The dashed lines are the traces of axial surfaces. [18.20]

In a geometric model of fault-propagation folds (Figure 8.33), the fault tip propagates up section as the fold’s backlimb and forelimb lengthen. The fault tip and the merge point of the fold’s kink axes lie at the same stratigraphic horizon. As in the fault-bend fold model, the backlimb of a fault-propagation fold parallels the dip of the ramp, and strata in the footwall remain flat-lying. In some cases, strata move through the kink axes as the fold evolves.

Detachment Folds

Folds may develop in fold-thrust belts above a detachment fault, even if no ramps develop. This happens where the strata above the detachment buckle or wrinkle up like a rug that has been shoved across a slick wooden floor (Figure 8.34).

FIGURE 8.34. Cross section of detachment folds in the foreland of the Jura Mountains (Switzerland). Note that the folds do not involve the pre-Triassic basement. The fold cores filled with weaker rock as the folds formed above the basal detachment (or décollement).

Detachment folds are particularly common in regions where detachments lie within thick shale or salt layers, as occurs in the Jura Mountains of Switzerland, for the weak rock can flow into the core of the fold as the structure develops. In some cases, a break thrust may develop at a late stage in the evolution of the fold; the fault cuts across the forelimb of the already formed detachment fold.

Division of folds in fold-thrust belts into the classes above is an oversimplification; instead, an evolutionary continuum exists between these classes. For example, initial detachment folding may establish the spacing for folds. Further shortening causes fold amplification and tightening, with the initiation and propagation of a break thrust further modifying the overall fold geometry. If displacement along the fault is sufficiently high, the fault may break through the fold forelimb, transporting the fold along the fault. If the thrust merges up dip with a flat, then continued displacement of the thrust sheet will cause the fold to evolve into a fault-bend fold. Alternatively, a fault may cease to grow and shortening in the area is accommodated by folding rather than by sliding on the fault surface.

SUPERPOSED FOLDING

Structural geologists use the term fold generation to refer to groups of folds that formed at approximately the same time interval and under similar kinematic conditions. Commonly we find several fold generations in an area, which are labeled by the letter F (for Fold) and a number reflecting the relative order of their formation: F1 folds form first, followed by F2 folds, F3 folds, and so on. Several fold generations may in turn form during an orogenic phase (such as the Siluro-Devonian “Acadian” phase in the Appalachians or the Cretaceous-Tertiary “Sevier” phase in the North American Cordillera), which is noted by the letter D (for Deformation phase). Several deformation phases may have occurred, which are labeled D1, D2, and so on, each containing one or more generations of folds.

From the onset it is important to emphasize that neither a deformation phase nor each of the individual fold generations have to be present everywhere along the orogen, nor do they occur everywhere at the same time. On a regional scale deformation is irregularly distributed and commonly diachronous. You can imagine that fold generations and deformation phase can rapidly become pretty complex. So we’ll stick to two fold generations to examine the principles of superposed folding, which allows us to unravel the sequence (that is, relative timing) of folding. Generation is a relative time concept and only implies “older than” or “younger than”; you are the younger generation in the eyes of your parents, and they are in the eyes of your grandparents. Today there are geochronologic methods to determine the absolute age of folds, such as dating of minerals that formed during folding, but we will not get into them here.

The relative time principle of superposed folding is simple: folds of a later generation are superimposed on folds of an earlier generation. The determination of this temporal sequence, however, is not straightforward and requires careful spatial analysis. Superposed folding is a widespread phenomenon that is not restricted to high-grade metamorphic areas. Even in regions below the greenschist facies (temperatures below ∼300°C), superposed folding is found. It is worthwhile therefore to give attention to this topic, after which we close this section with the concept of fold style that is used to place our findings on fold generations in a regional context.

Principle of Fold Superposition

Figure 8.35 shows a field photograph of a complex fold geometry that preserves two fold generations, as we explore below.

FIGURE 8.35. Fold interference pattern of Type 3 (“zig-zag fold”) geometry from the European Alps (Switzerland). (Courtesy JG Ramsay) [10.22]

How do we know this from looking at the picture and how can we separate F1 and F2 folds in this pattern? Fold superposition is simple at its root, but the concept requires the ability to visualize and analyze sometimes very complex three-dimensional geometries. Let us first start with the rule: a superposed fold must be younger than the structure it folds. This merely restates the Law of Superposition such that it applies to folding. Unless a fold was present previously, it cannot be modified by a younger fold. How do we determine the criteria by which one obtains this temporal relationship? We begin with an example.

FIGURE 8.36. Dissecting a fold interference pattern. The cross sections show FA recumbent folds (a) that are overprinted by FB upright folds (b), producing the fold interference pattern in (c). [10.23]

Figure 8.36a shows a sequence of recumbent folds that we will call FA; the associated axial surface is called SA. We now superimpose a series of upright folds of approximately the same scale (FB with axial surface SB; Figure 8.36c). The superimposition of FB on FA produces the interference pattern shown in Figure 8.36b. Elements of both fold generations are preserved; for example, the recumbent nature of FA is still there, but its limbs are now folded. Similarly, the upright FB folds remain visible, but they are superposed on a pattern that repeats and inverts bedding (from the recumbent FA folds). The way to determine the temporal relationship from our interference pattern is to invoke the rule of superposition. Both the bedding and SA are folded, but SB is essentially planar. So, bedding and SA were already present before SB; consequently, the upright folds must be F2, which are younger than the recumbent F1 folds. The axial surfaces may not be always visible in the field (although axial plane foliations are common; Chapter X), but you can always use an imaginary axial surface to evaluate these complex folding patterns. Now examine this pattern yourself with an analog. Take a piece of paper and fold it in two (our F1 fold) and orient it into a recumbent orientation. Then fold the paper again to create an upright fold (our F2 fold) whose hinge parallels the hinge of the recumbent fold. Voilà, you get the pattern of Figure 10.23b. If you are comfortable with this example, we will proceed with the four basic fold interference patterns.

Fold Interference Patterns

We recognize four basic types from the superimposition of upright F2 folds on pre-existing F1 folds with variable orientation (Figure 8.37). Looking at these fold interference types you will notice that we just produced Type 3 using the piece of folded paper above.

FIGURE 8.37. The four basic patterns arising from fold superposition. The analysis assumes that F2 folds (a2 is the relative displacement direction and b2 is the hinge line) are superimposed on a pre-existing F1 fold of variable orientation. The dark surface is the S1 axial surface. [10.24] [Interactive]

Types 0 and 2 can equally well be examined by folding a piece of paper, but Type 1 requires additional crumpling. Instead of describing these patterns in confusing words, look at Figure 8.37 and reproduce the geometries with a piece of paper and your hands. An approach that may offer further insight is to make fold interference patterns using a few thin layers of colored modeling clay, which can then be cut with a knife to see the effect of intersecting surfaces. Open a refreshing drink and start your experimentation. . . .

Welcome back from spending time with clay, paper, and Figure 8.37. We now turn to some important properties of the various fold interference types. Type 0 is a special condition, because the hinge lines and the axial surfaces of both fold generations are parallel. As a consequence, F1 is merely tightened by the superimposition of F2 (Figure 8.37a). You realize that, practically, Type 0 cannot be recognized in the field as an interference type by geometry alone (that’s why we use the number 0). Type 1 pattern is called “egg carton” structure as it resembles an egg carton. Both the axial surfaces and the hinge lines of the two generations are perpendicular, producing this characteristic geometry (Figure 8.37b). Type 2 is perhaps the most difficult geometry to visualize, but folding a piece of paper helps enormously. In outcrop, we often see a section through this geometry that resembles a “mushroom” pattern, hence its name (Figure 8.37c). Note that this outcrop pattern is only generated in the horizontal surface that intersects Type 2; if we take another cut, say vertical, the outcrop pattern is quite different. Type 3 (Figure 8.37d) is sometimes referred to as the “zig-zag” pattern. We recommend that you use the descriptive terms “egg carton” “mushroom,” and “zig-zag” folds, however flawed, instead of the abstract Type 1, Type 2, and Type 3, respectively.

Fold interference patterns are a function of the spatial relationship between hinge lines and axial surfaces of the fold generations, as well as the sectional surface in which we view the resulting patterns. Thus, the analysis of fold superposition is a three-dimensional problem. The four types that are shown in Figure 8.37 are only end-member configurations in an infinite array of possibilities. Interactive programs (such as “Visible Geology”) are available to explore the patterns from varying the spatial relationships between fold generations, as well as the observation surface (that is, the outcrop).

The fold interference patterns we have analyzed are produced when fold generations of similar scale are superimposed. If the scales are very different there may be no interference pattern visible on the outcrop scale, and only through regional structural analysis does the large-scale structure appear. After some field work it is therefore not uncommon to find one or more additional fold generations that only show on the map scale. A reexamination of some puzzling field notes and outcrop sketches may all of a sudden be explained by recognizing this missing fold generation.

The presence of multiple fold generations has major implications for the interpretation of the deformation history of your area. First, it implies that the kinematic conditions have changed to produce a fold generation with different orientation than before (except Type 0); so the deformation regime must somehow have changed. Secondly, folds of the first generation will have variable orientations depending on where they are measured in the fold superposition pattern. Orientation, therefore, is not a characteristic of fold generations in multiply deformed areas and should be used carefully as a mapping tool (see below). That leaves a final question: How do we recognize folds of a certain generation in the absence of interference patterns at each and every locality in our area? For this we introduce to the powerful concept of fold style.

Elements of Fold Style

When we encounter a number of folds in our field area, the logical question of their significance arises. Are they part of the same generation or do they represent several generations? Say that, at one locality in our area, we are actually able to determine a sequence of F1 and F2 folds, so we know that there are at least two generations. From our experience with superposed folding, we are also aware that only F2 folds have an orientation that may persist over any distance, and that the orientation of F1 folds depends entirely on their position in the fold interference pattern (we measure their orientation nonetheless because the distribution should “fit” the pattern). We now are at an outcrop where we only find one fold, which is not in the exact same orientation as either F1 or F2 in the previous outcrop. Nonetheless we wish to predict to which generation it belongs, and for that we use characteristics for each fold generation that are grouped under the term fold style. The fold style characteristics are:

In profile plane, is the fold classified as parallel or similar (or a further refinement)?
What is the interlimb angle in profile?
In three dimensions, is the fold cylindrical or non-cylindrical?
Is there an associated axial plane foliation and/or lineation present, and of what type?

The first three elements of fold style have already been discussed in detail and need no further clarification. Foliations and lineations will have more meaning after you read Chapter X, but this fourth characteristic is mentioned now because of its discriminatory ability. For example, an axial plane crenulation cleavage may be a characteristic of F2 folds, or the presence of a mineral lineation may reflect special metamorphic conditions that only occurred during F1.

Notably absent in our list are fold orientation and fold symmetry, which are not style criteria. Discriminating a fold generation on its orientation may only work for the last fold generation; the older ones most likely have become variably oriented. Secondly, we already learned that fold symmetry may change within a single-generation, large fold (Figure 10.16). So, just like orientation, symmetry is not a fold style criterion.

Fold Transposition

Folds are common in high strain zones, but often with a somewhat hidden appearance. In Figure 8.38 an asymmetric fold is formed from a small instability by foliation-parallel shear. With increasing shear, the oblique (short) limb of the asymmetric fold rotates back into a foliation-parallel orientation.

FIGURE 8.38. Fold transposition in a layered rock that undergoes non-coaxial, layer-parallel displacement. An asymmetric fold develops at a perturbation (a–d), which in turn gets refolded (e–f). The end result is a superimposed fold structure that is essentially parallel to the dominant layering. Note that if the second fold had formed at another location, the two would have been indistinguishable, although formed at different times. [12.24]

The resulting perturbation gives rise to a new fold that is superimposed on the original structure. Continued shear reorients the fold pattern back into a layer-parallel orientation (Figure 8.38e–f), leaving behind a complex geometry that can only be interpreted by carefully tracing the layering (Figure 8.39).

FIGURE 8.39. Transposed mafic layer in a granitic gneiss (Grenville Orogen, Ontario, Canada). The mafic (dark) layer can be traced as a single bed that is refolded numerous times in the outcrop (a). A detail of the large structure, which is affectionately known as the “snake outcrop,” highlights the complexity of folding; 2+m person for scale. [12.25]

This scenario, called fold transposition, highlights two aspects of folds in shear zones:

Fold asymmetry may be representative for the sense of shear; that is, Z-vergence occurs in right-lateral shear zones while S-vergence occurs in left-lateral shear zones. We state this only as a possibility and not as a rule, because at high shear strains the vergence of small folds may actually reverse (Figure 8.40).

FIGURE 8.40. Schematic illustration of reversal in fold vergence (from “S-shape” to “Z-shape”), with increasing shear strain in a right-lateral shear zone. [12.26]

Folding is a progressive process, resulting in complex patterns of folding and refolding. Fold transposition occurs at all scales, from micro-folds to kilometer-scale folds, and is, in fact, not restricted to zones of non-coaxial strain.

Folds in areas of high strain are often disrupted, preserving only isolated fold hinges or fold hooks (so called because of their resemblance to fishing hooks). Consider shortening that occurs parallel to competent layers in a less competent matrix, say sandstone layers in a shale matrix. The result is folds with an upright axial surface (Figure 8.41a); the fold enveloping surface is drawn for reference. Progressive shortening produces thinning of limbs and, locally, hinges become detached (Figure 8.41b; a natural example of this stage is shown in 8.41d). Eventually, we are left with a rock texture that is characterized by a single layering with lenses of more competent material (Figure 8.41c).

FIGURE 8.41. Fold transposition. Progressive coaxial strain (a–c) results in isoclinal folds that become disrupted by limb attenuation and boudinage. The enveloping surface is shown for reference. (d) A natural example of an early stage of transposition (Taiwan); hat for scale. [12.27]

Without knowledge of the history, the fabric in Figure 8.41c shows little or no indication of the original geometry, especially if the structures are very large (say kilometers). A cursory examination would suggest that overall bedding is up and down, until you notice the presence of the small fold hooks and maybe minor isoclinal folds. Only then do you realize that fold transposition has occurred. Transposed fabrics are even more pronounced when an axial plane foliation is formed, which will be nearly parallel to transposed layering. As a consequence, pretty much all layering in the rock seems parallel, with the exception of preserved fold hinges. Transposition in non-coaxial shear zones similarly results in a geometry in which all layering is roughly parallel to the shear-zone boundary. Try to sketch the evolution of folds in a non-coaxial environment, using Figure 8.40 as a starting point, and track the orientation of the enveloping surface for comparison with the coaxial strain scenario in Figure 8.41.

Rather than being the exception, transposition is more likely the rule in deformed metamorphic areas, where it is promoted by the overall weakness of layers at elevated pressures and temperatures. In addition to unraveling the deformation history, identifying transposition is important if you wish to erect a regional stratigraphy for an area, because it poses the question of whether repetition of a particular lithology is primary or structural in origin. So, are there criteria to recognize transposition? One clue is a regular repetition of lithologies; for example, repeated marble layers in an area of mafic gneisses may, on a regional scale, outline large transposed folds. When a sequence of lithologies exists, say gabbroic gneiss - marble, its repetition in reversing order is suggestive of transposition. Parallelism between foliation and bedding is not diagnostic by itself, but it should make you suspicious. The occurrence of minor isoclinal folds and fold hooks (especially if the foliation is axial-planar to these structures) adds weight to the case. You wrap up the interpretation by showing reversals in the direction of younging in layers across the area changes. Unfortunately, younging evidence is hard to find in medium- to high-grade metamorphic areas, but in low-grade metamorphic areas (greenschist facies and below) the observant geologist often finds evidence for younging.

Your efforts to prove a case of transposition will often bear fruit. Transposition results in a radical reinterpretation of stratigraphic relationships by showing that “stratigraphy” in the area is, in fact, structural in origin, and that the real stratigraphy is simpler. Secondly, a previously unrecognized early stage of isoclinal folding has major implications for the structural evolution of the area. Exhumed rocks in most (all?) of the world’s mountain belts show early stages of large-scale isoclinal folding, typically associated with thrusting, which is manifested in outcrop by fold transposition.

Sheath Folds

In closing this section on fold transposition, we describe one particular type of fold that is restricted to regions of very high shear, called sheath folds, or, more evocatively, condom folds. In contrast to the ambiguity of fold vergence in shear zones (Chapter 10), sheath folds can preserve displacement sense. These folds are typically exposed as eye-shaped outcrop patterns that reflect a section through the nose of the fold (Figure 8.42).

FIGURE 8.42. (a) Sheath fold in amphibolite gneiss showing the characteristic eye-shaped outcrop pattern (Grenville Orogen, Ontario, Canada); hammer for scale. (b) Sheath folds form when weakly doubly-plunging folds are modified in a zone of high shear strain, with the most evolved stage producing the characteristic conical geometry (fold 4). The progression shows the lowest shear at left and the highest shear strain at right. Note the progressive curvature of the hinge line in folds 1 to 3, which often is accompanied by a (stretching) lineation in outcrop. Corresponding lower-hemisphere projections of hinge lines in folds 1, 2, and 3 are shown. The great circle represents the shear plane and the open circle the shear direction; small dots are hinge-line measurements. [12.28]

Sheath folds can be seen as a special type of doubly plunging folds, except that the hinge line is bent around by as much as 180°. In other words, layering in a sheath fold is everywhere at a high angle to the profile plane, which gives the characteristic eye-shaped outcrop pattern. Sheath folds are formed when the hinge line of a fold rotates passively into the direction of shear, while the axial surface rotates toward the shear plane (Figure 8.42b). Note that sheath folds differ from “dome-and-basin” type fold interference patterns, because they form by progressive strain under the same overall deformation regime, rather than reflecting two discrete deformation regimes. Since hinge rotations require high amounts of shear strain, the occurrence of sheath folds in crustal rocks is limited to mylonites.

The degree of hinge rotation is a function of shear strain and the angular relationship of hinge line with the shear plane. However, sheath folds cannot be used as a strain gauge beyond the general comment of “large amount of shear,” unless these initial angular relationships are known. When fully exposed, sheath folds can be used as a shear-sense indicator with the nose pointing in the direction of transport; otherwise, sheath folds indicate the direction of shear only. In less-rotated portions of a sheath fold, the shear sense may also be derived from hinge line rotation (Figure 8.42b). Most commonly, sheath folds give the direction of shear rather than shear sense, with the hinge line approximately parallel to the displacement direction.

A Practical Note

We close the section on superposed folding with a few considerations. You will often find that it is not possible in any single outcrop to determine the complete sequence of fold generations, because discriminatory interference patterns may not be exposed, or one or more generations may not be visible at all. However, by combining information from several outcrops as well as using fold style you should eventually be able to obtain a reasonable fold sequence. As you map, you should continue to test this hypothesis, and after a thorough job the foundation on which you base the folding sequence will be firm. Only then will the time have come to place your findings in a regional kinematic picture. For example, you may find that the first generation of folds is recumbent, which we quite commonly associate with nappe style, and that the second fold generation is upright, reflecting folding of the thrust sequence. Maybe yet a third fold generation reflects a very different shortening direction, possibly related to a different orogenic phase. We may also find small kink folds in well-foliated rocks that complete the deformation sequence. Although the possibilities seem limitless, reasonable interpretations are not. There is sometimes a tendency to recognize too many fold generations by structural geologists. In the end, the number of fold generations should be based only on interference patterns, on either local or regional scales. Practically, in any one outcrop you may be able to see two or three fold generations, and regionally perhaps a couple more. Remember that structural analysis is not helped by proposing an unnecessarily long and complex sequence of fold generations, because each generation must reflect a corresponding deformation regime. One can reasonably expect only so many different tectonic patterns.

Back to Folds and Folding Contents

Back to PSG&T Home

v1.2; Last update: 15-Sep-2023

[1] Sometimes fold axis is used as a synonym for hinge line, but this is not technically correct.

[2] Just look at your neighbor’s sketch.

[3] This does not necessarily reflect the authors’ personal experiences.

[4] Biot and Ramberg independently carried out this analysis in the early 1960s.